7 The Electric Field in Various Circumstances (Continued)
The Electric Field in Various Circumstances (Continued)
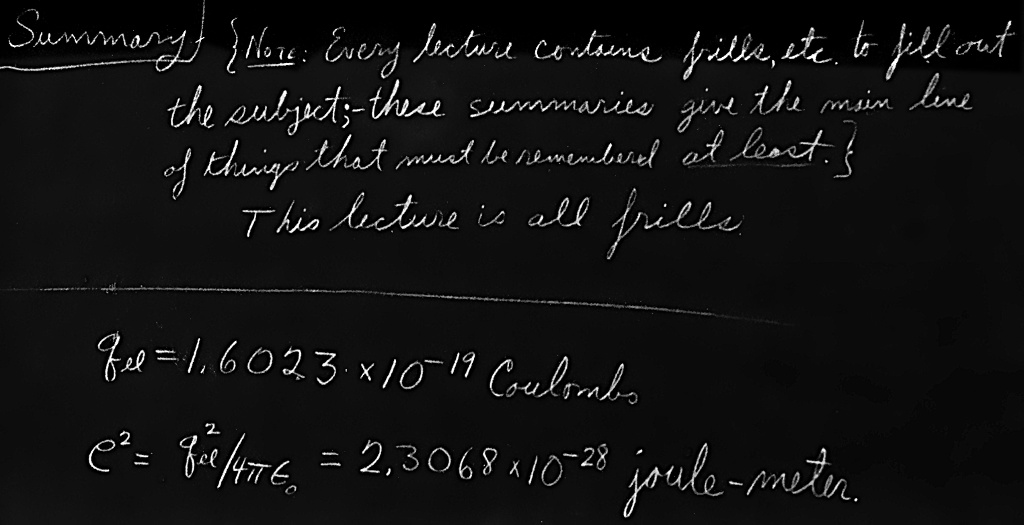
7–1Methods for finding the electrostatic field
This chapter is a continuation of our consideration of the characteristics of electric fields in various particular situations. We shall first describe some of the more elaborate methods for solving problems with conductors. It is not expected that these more advanced methods can be mastered at this time. Yet it may be of interest to have some idea about the kinds of problems that can be solved, using techniques that may be learned in more advanced courses. Then we take up two examples in which the charge distribution is neither fixed nor is carried by a conductor, but instead is determined by some other law of physics.
As we found in Chapter 6, the problem of the electrostatic field is fundamentally simple when the distribution of charges is specified; it requires only the evaluation of an integral. When there are conductors present, however, complications arise because the charge distribution on the conductors is not initially known; the charge must distribute itself on the surface of the conductor in such a way that the conductor is an equipotential. The solution of such problems is neither direct nor simple.
We have looked at an indirect method of solving such problems, in which we find the equipotentials for some specified charge distribution and replace one of them by a conducting surface. In this way we can build up a catalog of special solutions for conductors in the shapes of spheres, planes, etc. The use of images, described in Chapter 6, is an example of an indirect method. We shall describe another in this chapter.
If the problem to be solved does not belong to the class of problems for which we can construct solutions by the indirect method, we are forced to solve the problem by a more direct method. The mathematical problem of the direct method is the solution of Laplace’s equation, \begin{equation} \label{Eq:II:7:1} \nabla^2\phi=0, \end{equation} subject to the condition that $\phi$ is a suitable constant on certain boundaries—the surfaces of the conductors. Problems which involve the solution of a differential field equation subject to certain boundary conditions are called boundary-value problems. They have been the object of considerable mathematical study. In the case of conductors having complicated shapes, there are no general analytical methods. Even such a simple problem as that of a charged cylindrical metal can closed at both ends—a beer can—presents formidable mathematical difficulties. It can be solved only approximately, using numerical methods. The only general methods of solution are numerical.
There are a few problems for which Eq. (7.1) can be solved directly. For example, the problem of a charged conductor having the shape of an ellipsoid of revolution can be solved exactly in terms of known special functions. The solution for a thin disc can be obtained by letting the ellipsoid become infinitely oblate. In a similar manner, the solution for a needle can be obtained by letting the ellipsoid become infinitely prolate. However, it must be stressed that the only direct methods of general applicability are the numerical techniques.
Boundary-value problems can also be solved by measurements of a physical analog. Laplace’s equation arises in many different physical situations: in steady-state heat flow, in irrotational fluid flow, in current flow in an extended medium, and in the deflection of an elastic membrane. It is frequently possible to set up a physical model which is analogous to an electrical problem which we wish to solve. By the measurement of a suitable analogous quantity on the model, the solution to the problem of interest can be determined. An example of the analog technique is the use of the electrolytic tank for the solution of two-dimensional problems in electrostatics. This works because the differential equation for the potential in a uniform conducting medium is the same as it is for a vacuum.
There are many physical situations in which the variations of the physical fields in one direction are zero, or can be neglected in comparison with the variations in the other two directions. Such problems are called two-dimensional; the field depends on two coordinates only. For example, if we place a long charged wire along the $z$-axis, then for points not too far from the wire the electric field depends on $x$ and $y$, but not on $z$; the problem is two-dimensional. Since in a two-dimensional problem $\ddpl{\phi}{z}=0$, the equation for $\phi$ in free space is \begin{equation} \label{Eq:II:7:2} \frac{\partial^2\phi}{\partial x^2}+ \frac{\partial^2\phi}{\partial y^2}=0. \end{equation} Because the two-dimensional equation is comparatively simple, there is a wide range of conditions under which it can be solved analytically. There is, in fact, a very powerful indirect mathematical technique which depends on a theorem from the mathematics of functions of a complex variable, and which we will now describe.
7–2Two-dimensional fields; functions of the complex variable
The complex variable $\frakz$ is defined as \begin{equation*} \frakz=x+iy. \end{equation*} (Do not confuse $\frakz$ with the $z$-coordinate, which we ignore in the following discussion because we assume there is no $z$-dependence of the fields.) Every point in $x$ and $y$ then corresponds to a complex number $\frakz$. We can use $\frakz$ as a single (complex) variable, and with it write the usual kinds of mathematical functions $F(\frakz)$. For example, \begin{equation*} F(\frakz) =\frakz^2, \end{equation*} or \begin{equation*} F(\frakz) =1/\frakz^3, \end{equation*} or \begin{equation*} F(\frakz) =\frakz\ln\frakz, \end{equation*} and so forth.
Given any particular $F(\frakz)$ we can substitute $\frakz=x+iy$, and we have a function of $x$ and $y$—with real and imaginary parts. For example, \begin{equation} \label{Eq:II:7:3} \frakz^2=(x+iy)^2=x^2-y^2+2ixy. \end{equation}
Any function $F(\frakz)$ can be written as a sum of a pure real part and a pure imaginary part, each part a function of $x$ and $y$: \begin{equation} \label{Eq:II:7:4} F(\frakz)=U(x,y)+iV(x,y), \end{equation} where $U(x,y)$ and $V(x,y)$ are real functions. Thus from any complex function $F(\frakz)$ two new functions $U(x,y)$ and $V(x,y)$ can be derived. For example, $F(\frakz)=\frakz^2$ gives us the two functions \begin{equation} \label{Eq:II:7:5} U(x,y) =x^2-y^2, \end{equation} and \begin{equation} \label{Eq:II:7:6} V(x,y) =2xy. \end{equation}
Now we come to a miraculous mathematical theorem which is so delightful that we shall leave a proof of it for one of your courses in mathematics. (We should not reveal all the mysteries of mathematics, or that subject matter would become too dull.) It is this. For any “ordinary function” (mathematicians will define it better) the functions $U$ and $V$ automatically satisfy the relations \begin{align} \label{Eq:II:7:7} \ddp{U}{x}&=\ddp{V}{y},\\[1ex] \label{Eq:II:7:8} \ddp{V}{x}&=-\ddp{U}{y}. \end{align} It follows immediately that each of the functions $U$ and $V$ satisfy Laplace’s equation: \begin{align} \label{Eq:II:7:9} \frac{\partial^2 U}{\partial x^2}+ \frac{\partial^2 U}{\partial y^2}&=0,\\[1ex] \label{Eq:II:7:10} \frac{\partial^2 V}{\partial x^2}+ \frac{\partial^2 V}{\partial y^2}&=0, \end{align} These equations are clearly true for the functions of (7.5) and (7.6).
Thus, starting with any ordinary function, we can arrive at two functions $U(x,y)$ and $V(x,y)$, which are both solutions of Laplace’s equation in two dimensions. Each function represents a possible electrostatic potential. We can pick any function $F(\frakz)$ and it should represent some electric field problem—in fact, two problems, because $U$ and $V$ each represent solutions. We can write down as many solutions as we wish—by just making up functions—then we just have to find the problem that goes with each solution. It may sound backwards, but it’s a possible approach.
As an example, let’s see what physics the function $F(\frakz)=\frakz^2$ gives us. From it we get the two potential functions of (7.5) and (7.6). To see what problem the function $U$ belongs to, we solve for the equipotential surfaces by setting $U=A$, a constant: \begin{equation*} x^2-y^2=A. \end{equation*} This is the equation of a rectangular hyperbola. For various values of $A$, we get the hyperbolas shown in Fig. 7–1. When $A=0$, we get the special case of diagonal straight lines through the origin.
Such a set of equipotentials corresponds to the field at an inside right-angle corner of a conductor. If we have two electrodes shaped like those in Fig. 7–2, which are held at different potentials, the field near the corner marked $C$ will look just like the field above the origin in Fig. 7–1. The solid lines are the equipotentials, and the broken lines at right angles correspond to lines of $\FLPE$. Whereas at points or protuberances the electric field tends to be high, it tends to be low in dents or hollows.
The solution we have found also corresponds to that for a hyperbola-shaped electrode near a right-angle corner, or for two hyperbolas at suitable potentials. You will notice that the field of Fig. 7–1 has an interesting property. The $x$-component of the electric field, $E_x$, is given by \begin{equation*} E_x=-\ddp{\phi}{x}=-2x. \end{equation*} The electric field is proportional to the distance from the axis. This fact is used to make devices (called quadrupole lenses) that are useful for focusing particle beams (see Section 29–7). The desired field is usually obtained by using four hyperbola shaped electrodes, as shown in Fig. 7–3. For the electric field lines in Fig. 7–3, we have simply copied from Fig. 7–1 the set of broken-line curves that represent $V=\text{constant}$. We have a bonus! The curves for $V=\text{constant}$ are orthogonal to the ones for $U=\text{constant}$ because of the equations (7.7) and (7.8). Whenever we choose a function $F(\frakz)$, we get from $U$ and $V$ both the equipotentials and field lines. And you will remember that we have solved either of two problems, depending on which set of curves we call the equipotentials.
As a second example, consider the function \begin{equation} \label{Eq:II:7:11} F(\frakz)=\sqrt{\frakz}. \end{equation} If we write \begin{equation} \frakz=x+iy=\rho e^{i\theta},\notag \end{equation} where \begin{equation} \rho=\sqrt{x^2+y^2}\notag \end{equation} and \begin{equation} \tan\theta=y/x,\notag \end{equation} then \begin{equation} \begin{aligned} F(\frakz)&=\rho^{1/2}e^{i\theta/2}\\ &=\rho^{1/2}\biggl(\cos\frac{\theta}{2}+i\sin\frac{\theta}{2}\biggr), \end{aligned}\notag \end{equation} from which \begin{equation} \label{Eq:II:7:12} F(\frakz)=\biggl[\frac{(x^2+y^2)^{1/2}+x}{2}\biggr]^{1/2}\kern{-1.5ex}+ i\biggl[\frac{(x^2+y^2)^{1/2}-x}{2}\biggr]^{1/2}. \end{equation} \begin{equation} \begin{aligned} F(\frakz)=&\biggl[\frac{(x^2\!+y^2)^{1/2}\!+x}{2}\biggr]^{1/2}\notag\\[1ex] &+\,i\biggl[\frac{(x^2\!+y^2)^{1/2}\!-x}{2}\biggr]^{1/2}\!. \end{aligned} \label{Eq:II:7:12} \end{equation}
The curves for $U(x,y)=A$ and $V(x,y)=B$, using $U$ and $V$ from Eq. (7.12), are plotted in Fig. 7–4. Again, there are many possible situations that could be described by these fields. One of the most interesting is the field near the edge of a thin plate. If the line $B=0$—to the right of the $y$-axis—represents a thin charged plate, the field lines near it are given by the curves for various values of $A$. The physical situation is shown in Fig. 7–5.
Further examples are \begin{equation} \label{Eq:II:7:13} F(\frakz)=\frakz^{2/3}, \end{equation} which yields the field outside a rectangular corner \begin{equation} \label{Eq:II:7:14} F(\frakz)=\ln\frakz, \end{equation} which yields the field for a line charge, and \begin{equation} \label{Eq:II:7:15} F(\frakz)=1/\frakz, \end{equation} which gives the field for the two-dimensional analog of an electric dipole, i.e., two parallel line charges with opposite polarities, very close together.
We will not pursue this subject further in this course, but should emphasize that although the complex variable technique is often powerful, it is limited to two-dimensional problems; and also, it is an indirect method.
7–3Plasma oscillations
We consider now some physical situations in which the field is determined neither by fixed charges nor by charges on conducting surfaces, but by a combination of two physical phenomena. In other words, the field will be governed simultaneously by two sets of equations: (1) the equations from electrostatics relating electric fields to charge distribution, and (2) an equation from another part of physics that determines the positions or motions of the charges in the presence of the field.
The first example that we will discuss is a dynamic one in which the motion of the charges is governed by Newton’s laws. A simple example of such a situation occurs in a plasma, which is an ionized gas consisting of ions and free electrons distributed over a region in space. The ionosphere—an upper layer of the atmosphere—is an example of such a plasma. The ultraviolet rays from the sun knock electrons off the molecules of the air, creating free electrons and ions. In such a plasma the positive ions are very much heavier than the electrons, so we may neglect the ionic motion, in comparison to that of the electrons.
Let $n_0$ be the density of electrons in the undisturbed, equilibrium state. Assuming the molecules are singly ionized, this must also be the density of positive ions, since the plasma is electrically neutral (when undisturbed). Now we suppose that the electrons are somehow moved from equilibrium and ask what happens. If the density of the electrons in one region is increased, they will repel each other and tend to return to their equilibrium positions. As the electrons move toward their original positions they pick up kinetic energy, and instead of coming to rest in their equilibrium configuration, they overshoot the mark. They will oscillate back and forth. The situation is similar to what occurs in sound waves, in which the restoring force is the gas pressure. In a plasma, the restoring force is the electrical force on the electrons.
To simplify the discussion, we will worry only about a situation in which the motions are all in one dimension, say $x$. Let us suppose that the electrons originally at $x$ are, at the instant $t$, displaced from their equilibrium positions by a small amount $s(x,t)$. Since the electrons have been displaced, their density will, in general, be changed. The change in density is easily calculated. Referring to Fig. 7–6, the electrons initially contained between the two planes $a$ and $b$ have moved and are now contained between the planes $a'$ and $b'$. The number of electrons that were between $a$ and $b$ is proportional to $n_0\Delta x$; the same number are now contained in the space whose width is $\Delta x+\Delta s$. The density has changed to \begin{equation} \label{Eq:II:7:16} n=\frac{n_0\Delta x}{\Delta x+\Delta s}=\frac{n_0}{1+(\Delta s/\Delta x)}. \end{equation} If the change in density is small, we can write [using the binomial expansion for $(1+\epsilon)^{-1}$] \begin{equation} \label{Eq:II:7:17} n=n_0\biggl(1-\frac{\Delta s}{\Delta x}\biggr). \end{equation} We assume that the positive ions do not move appreciably (because of the much larger inertia), so their density remains $n_0$. Each electron carries the charge $-q_e$, so the average charge density at any point is given by \begin{equation} \rho =-(n-n_0)q_e,\notag \end{equation} or \begin{equation} \label{Eq:II:7:18} \rho =n_0q_e\,\frac{ds}{dx} \end{equation} (where we have written the differential form for $\Delta s/\Delta x$).
The charge density is related to the electric field by Maxwell’s equations, in particular, \begin{equation} \label{Eq:II:7:19} \FLPdiv{\FLPE}=\frac{\rho}{\epsO}. \end{equation} If the problem is indeed one-dimensional (and if there are no other fields but the one due to the displacements of the electrons), the electric field $\FLPE$ has a single component $E_x$. Equation (7.19), together with (7.18), gives \begin{equation} \label{Eq:II:7:20} \ddp{E_x}{x}=\frac{n_0q_e}{\epsO}\,\ddp{s}{x}. \end{equation} Integrating Eq. (7.20) gives \begin{equation} \label{Eq:II:7:21} E_x=\frac{n_0q_e}{\epsO}\,s+K. \end{equation} Since $E_x=0$ when $s=0$, the integration constant $K$ is zero.
The force on an electron in the displaced position is \begin{equation} \label{Eq:II:7:22} F_x=-\frac{n_0q_e^2}{\epsO}\,s, \end{equation} a restoring force proportional to the displacement $s$ of the electron. This leads to a harmonic oscillation of the electrons. The equation of motion of a displaced electron is \begin{equation} \label{Eq:II:7:23} m_e\frac{d^2s}{dt^2}=-\frac{n_0q_e^2}{\epsO}\,s. \end{equation} We find that $s$ will vary harmonically. Its time variation will be as $\cos\omega_pt$, or—using the exponential notation of Vol. I—as \begin{equation} \label{Eq:II:7:24} e^{i\omega_pt}. \end{equation} The frequency of oscillation $\omega_p$ is determined from (7.23): \begin{equation} \label{Eq:II:7:25} \omega_p^2=\frac{n_0q_e^2}{\epsO m_e}, \end{equation} and is called the plasma frequency. It is a characteristic number of the plasma.
When dealing with electron charges many people prefer to express their answers in terms of a quantity $e^2$ defined by \begin{equation} \label{Eq:II:7:26} e^2=\frac{q_e^2}{4\pi\epsO}= 2.3068\times10^{-28}\text{ newton$\cdot$meter$^2$}. \end{equation} Using this convention, Eq. (7.25) becomes \begin{equation} \label{Eq:II:7:27} \omega_p^2=\frac{4\pi e^2n_0}{m_e}, \end{equation} which is the form you will find in most books.
Thus we have found that a disturbance of a plasma will set up free oscillations of the electrons about their equilibrium positions at the natural frequency $\omega_p$, which is proportional to the square root of the density of the electrons. The plasma electrons behave like a resonant system, such as those we described in Chapter 23 of Vol. I.
This natural resonance of a plasma has some interesting effects. For example, if one tries to propagate a radiowave through the ionosphere, one finds that it can penetrate only if its frequency is higher than the plasma frequency. Otherwise the signal is reflected back. We must use high frequencies if we wish to communicate with a satellite in space. On the other hand, if we wish to communicate with a radio station beyond the horizon, we must use frequencies lower than the plasma frequency, so that the signal will be reflected back to the earth.
Another interesting example of plasma oscillations occurs in metals. In a metal we have a contained plasma of positive ions, and free electrons. The density $n_0$ is very high, so $\omega_p$ is also. But it should still be possible to observe the electron oscillations. Now, according to quantum mechanics, a harmonic oscillator with a natural frequency $\omega_p$ has energy levels which are separated by the energy increment $\hbar\omega_p$. If, then, one shoots electrons through, say, an aluminum foil, and makes very careful measurements of the electron energies on the other side, one might expect to find that the electrons sometimes lose the energy $\hbar\omega_p$ to the plasma oscillations. This does indeed happen. It was first observed experimentally in 1936 that electrons with energies of a few hundred to a few thousand electron volts lost energy in jumps when scattering from or going through a thin metal foil. The effect was not understood until 1953 when Bohm and Pines1 showed that the observations could be explained in terms of quantum excitations of the plasma oscillations in the metal.
7–4Colloidal particles in an electrolyte
We turn to another phenomenon in which the locations of charges are governed by a potential that arises in part from the same charges. The resulting effects influence in an important way the behavior of colloids. A colloid consists of a suspension in water of small charged particles which, though microscopic, from an atomic point of view are still very large. If the colloidal particles were not charged, they would tend to coagulate into large lumps; but because of their charge, they repel each other and remain in suspension.
Now if there is also some salt dissolved in the water, it will be dissociated into positive and negative ions. (Such a solution of ions is called an electrolyte.) The negative ions are attracted to the colloid particles (assuming their charge is positive) and the positive ions are repelled. We will determine how the ions which surround such a colloidal particle are distributed in space.
To keep the ideas simple, we will again solve only a one-dimensional case. If we think of a colloidal particle as a sphere having a very large radius—on an atomic scale!—we can then treat a small part of its surface as a plane. (Whenever one is trying to understand a new phenomenon it is a good idea to take a somewhat oversimplified model; then, having understood the problem with that model, one is better able to proceed to tackle the more exact calculation.)
We suppose that the distribution of ions generates a charge density $\rho(x)$, and an electrical potential $\phi$, related by the electrostatic law $\nabla^2\phi=-\rho/\epsO$ or, for fields that vary in only one dimension, by \begin{equation} \label{Eq:II:7:28} \frac{d^2\phi}{dx^2}=-\frac{\rho}{\epsO}. \end{equation}
Now supposing there were such a potential $\phi(x)$, how would the ions distribute themselves in it? This we can determine by the principles of statistical mechanics. Our problem then is to determine $\phi$ so that the resulting charge density from statistical mechanics also satisfies (7.28).
According to statistical mechanics (see Chapter 40, Vol. I), particles in thermal equilibrium in a force field are distributed in such a way that the density $n$ of particles at the position $x$ is given by \begin{equation} \label{Eq:II:7:29} n(x)=n_0e^{-U(x)/kT}, \end{equation} where $U(x)$ is the potential energy, $k$ is Boltzmann’s constant, and $T$ is the absolute temperature.
We assume that the ions carry one electronic charge, positive or negative. At the distance $x$ from the surface of a colloidal particle, a positive ion will have potential energy $q_e\phi(x)$, so that \begin{equation*} U(x)=q_e\phi(x). \end{equation*} The density of positive ions, $n_+$, is then \begin{equation*} n_+(x)=n_0e^{-q_e\phi(x)/kT}. \end{equation*} Similarly, the density of negative ions is \begin{equation*} n_-(x)=n_0e^{+q_e\phi(x)/kT}. \end{equation*} The total charge density is \begin{equation} \rho =q_en_+-q_en_-,\notag \end{equation} or \begin{equation} \label{Eq:II:7:30} \rho =q_en_0(e^{-q_e\phi/kT}-e^{+q_e\phi/kT}). \end{equation} Combining this with Eq. (7.28), we find that the potential $\phi$ must satisfy \begin{equation} \label{Eq:II:7:31} \frac{d^2\phi}{dx^2}=-\frac{q_en_0}{\epsO} (e^{-q_e\phi/kT}-e^{+q_e\phi/kT}). \end{equation} This equation is readily solved in general [multiply both sides by $2(d\phi/dx)$, and integrate with respect to $x$], but to keep the problem as simple as possible, we will consider here only the limiting case in which the potentials are small or the temperature $T$ is high. The case where $\phi$ is small corresponds to a dilute solution. For these cases the exponent is small, and we can approximate \begin{equation} \label{Eq:II:7:32} e^{\pm q_e\phi/kT}=1\pm\frac{q_e\phi}{kT}. \end{equation} Equation (7.31) then gives \begin{equation} \label{Eq:II:7:33} \frac{d^2\phi}{dx^2}=+\frac{2n_0q_e^2}{\epsO kT}\phi(x). \end{equation} Notice that this time the sign on the right is positive. The solutions for $\phi$ are not oscillatory, but exponential.
The general solution of Eq. (7.33) is \begin{equation} \label{Eq:II:7:34} \phi=Ae^{-x/D}+Be^{+x/D}, \end{equation} with \begin{equation} \label{Eq:II:7:35} D^2=\frac{\epsO kT}{2n_0q_e^2}. \end{equation} The constants $A$ and $B$ must be determined from the conditions of the problem. In our case, $B$ must be zero; otherwise the potential would go to infinity for large $x$. So we have that \begin{equation} \label{Eq:II:7:36} \phi=Ae^{-x/D}, \end{equation} in which $A$ is the potential at $x=0$, the surface of the colloidal particle.
The potential decreases by a factor $1/e$ each time the distance increases by $D$, as shown in the graph of Fig. 7–7. The number $D$ is called the Debye length, and is a measure of the thickness of the ion sheath that surrounds a large charged particle in an electrolyte. Equation (7.35) says that the sheath gets thinner with increasing concentration of the ions ($n_0$) or with decreasing temperature.
The constant $A$ in Eq. (7.36) is easily obtained if we know the surface charge density $\sigma$ on the colloid particle. We know that \begin{equation} \label{Eq:II:7:37} E_n=E_x(0)=\frac{\sigma}{\epsO}. \end{equation} But $\FLPE$ is also the gradient of $-\phi$: \begin{equation} \label{Eq:II:7:38} E_x(0)=-\left.\ddp{\phi}{x}\right|_0=+\frac{A}{D}, \end{equation} from which we get \begin{equation} \label{Eq:II:7:39} A=\frac{\sigma D}{\epsO}. \end{equation} Using this result in (7.36), we find (by taking $x=0$) that the potential of the colloidal particle is \begin{equation} \label{Eq:II:7:40} \phi(0)=\frac{\sigma D}{\epsO}. \end{equation} You will notice that this potential is the same as the potential difference across a condenser with a plate spacing $D$ and a surface charge density $\sigma$.
We have said that the colloidal particles are kept apart by their electrical repulsion. But now we see that the field a little way from the surface of a particle is reduced by the ion sheath that collects around it. If the sheaths get thin enough, the particles have a good chance of knocking against each other. They will then stick, and the colloid will coagulate and precipitate out of the liquid. From our analysis, we understand why adding enough salt to a colloid should cause it to precipitate out. The process is called “salting out a colloid.”
Another interesting example is the effect that a salt solution has on protein molecules. A protein molecule is a long, complicated, and flexible chain of amino acids. The molecule has various charges on it, and it sometimes happens that there is a net charge, say negative, which is distributed along the chain. Because of mutual repulsion of the negative charges, the protein chain is kept stretched out. Also, if there are other similar chain molecules present in the solution, they will be kept apart by the same repulsive effects. We can, therefore, have a suspension of chain molecules in a liquid. But if we add salt to the liquid we change the properties of the suspension. As salt is added to the solution, decreasing the Debye distance, the chain molecules can approach one another, and can also coil up. If enough salt is added to the solution, the chain molecules will precipitate out of the solution. There are many chemical effects of this kind that can be understood in terms of electrical forces.
7–5The electrostatic field of a grid
As our last example, we would like to describe another interesting property of electric fields. It is one which is made use of in the design of electrical instruments, in the construction of vacuum tubes, and for other purposes. This is the character of the electric field near a grid of charged wires. To make the problem as simple as possible, let us consider an array of parallel wires lying in a plane, the wires being infinitely long and with a uniform spacing between them.
If we look at the field a large distance above the plane of the wires, we see a constant electric field, just as though the charge were uniformly spread over a plane. As we approach the grid of wires, the field begins to deviate from the uniform field we found at large distances from the grid. We would like to estimate how close to the grid we have to be in order to see appreciable variations in the potential. Figure 7–8 shows a rough sketch of the equipotentials at various distances from the grid. The closer we get to the grid, the larger the variations. As we travel parallel to the grid, we observe that the field fluctuates in a periodic manner.
Now we have seen (Chapter 50, Vol. I) that any periodic quantity can be expressed as a sum of sine waves (Fourier’s theorem). Let’s see if we can find a suitable harmonic function that satisfies our field equations.
If the wires lie in the $xy$-plane and run parallel to the $y$-axis, then we might try terms like \begin{equation} \label{Eq:II:7:41} \phi(x,z)=F_n(z)\cos\frac{2\pi nx}{a}, \end{equation} where $a$ is the spacing of the wires and $n$ is the harmonic number. (We have assumed long wires, so there should be no variation with $y$.) A complete solution would be made up of a sum of such terms for $n=1$, $2$, $3$, $\dotsc$.
If this is to be a valid potential, it must satisfy Laplace’s equation in the region above the wires (where there are no charges). That is, \begin{equation*} \frac{\partial^2\phi}{\partial x^2}+ \frac{\partial^2\phi}{\partial z^2}=0. \end{equation*} Trying this equation on the $\phi$ in (7.41), we find that \begin{equation} \label{Eq:II:7:42} -\frac{4\pi^2n^2}{a^2}F_n(z)\cos\frac{2\pi nx}{a}+ \frac{d^2F_n}{dz^2}\cos\frac{2\pi nx}{a}=0, \end{equation} or that $F_n(z)$ must satisfy \begin{equation} \label{Eq:II:7:43} \frac{d^2F_n}{dz^2}=\frac{4\pi^2 n^2}{a^2}\,F_n. \end{equation} So we must have \begin{equation} \label{Eq:II:7:44} F_n=A_ne^{-z/z_0}, \end{equation} where \begin{equation} \label{Eq:II:7:45} z_0=\frac{a}{2\pi n}. \end{equation} We have found that if there is a Fourier component of the field of harmonic $n$, that component will decrease exponentially with a characteristic distance $z_0=a/2\pi n$. For the first harmonic ($n=1$), the amplitude falls by the factor $e^{-2\pi}$ (a large decrease) each time we increase $z$ by one grid spacing $a$. The other harmonics fall off even more rapidly as we move away from the grid. We see that if we are only a few times the distance $a$ away from the grid, the field is very nearly uniform, i.e., the oscillating terms are small. There would, of course, always remain the “zero harmonic” field \begin{equation*} \phi_0=-E_0z \end{equation*} to give the uniform field at large $z$. For a complete solution, we would combine this term with a sum of terms like (7.41) with $F_n$ from (7.44). The coefficients $A_n$ would be adjusted so that the total sum would, when differentiated, give an electric field that would fit the charge density $\lambda$ of the grid wires.
The method we have just developed can be used to explain why electrostatic shielding by means of a screen is often just as good as with a solid metal sheet. Except within a distance from the screen a few times the spacing of the screen wires, the fields inside a closed screen are zero. We see why copper screen—lighter and cheaper than copper sheet—is often used to shield sensitive electrical equipment from external disturbing fields.
- For some recent work and a bibliography see C. J. Powell and J. B. Swann, Phys. Rev. 115, 869 (1959). ↩