6 The Electric Field in Various Circumstances
The Electric Field in Various Circumstances
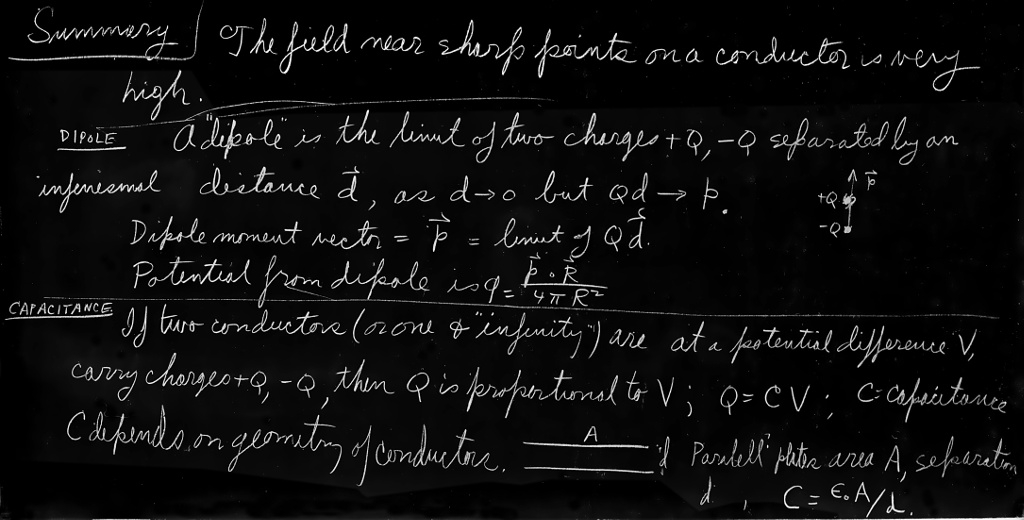
| Review: | Chapter 23, Vol. I, Resonance |
6–1Equations of the electrostatic potential
This chapter will describe the behavior of the electric field in a number of different circumstances. It will provide some experience with the way the electric field behaves, and will describe some of the mathematical methods which are used to find this field.
We begin by pointing out that the whole mathematical problem is the solution of two equations, the Maxwell equations for electrostatics: \begin{align} \label{Eq:II:6:1} \FLPdiv{\FLPE}&=\frac{\rho}{\epsO},\\[1ex] \label{Eq:II:6:2} \FLPcurl{\FLPE}&=\FLPzero. \end{align} In fact, the two can be combined into a single equation. From the second equation, we know at once that we can describe the field as the gradient of a scalar (see Section 3–7): \begin{equation} \label{Eq:II:6:3} \FLPE=-\FLPgrad{\phi}. \end{equation}
We may, if we wish, completely describe any particular electric field in terms of its potential $\phi$. We obtain the differential equation that $\phi$ must obey by substituting Eq. (6.3) into (6.1), to get \begin{equation} \label{Eq:II:6:4} \FLPdiv{\FLPgrad{\phi}}=-\frac{\rho}{\epsO}. \end{equation} The divergence of the gradient of $\phi$ is the same as $\nabla^2$ operating on $\phi$: \begin{equation} \label{Eq:II:6:5} \FLPdiv{\FLPgrad{\phi}}=\nabla^2\phi= \frac{\partial^2\phi}{\partial x^2}+ \frac{\partial^2\phi}{\partial y^2}+ \frac{\partial^2\phi}{\partial z^2}, \end{equation} so we write Eq. (6.4) as \begin{equation} \label{Eq:II:6:6} \nabla^2\phi=-\frac{\rho}{\epsO}. \end{equation} The operator $\nabla^2$ is called the Laplacian, and Eq. (6.6) is called the Poisson equation. The entire subject of electrostatics, from a mathematical point of view, is merely a study of the solutions of the single equation (6.6). Once $\phi$ is obtained by solving Eq. (6.6) we can find $\FLPE$ immediately from Eq. (6.3).
We take up first the special class of problems in which $\rho$ is given as a function of $x$, $y$, $z$. In that case the problem is almost trivial, for we already know the solution of Eq. (6.6) for the general case. We have shown that if $\rho$ is known at every point, the potential at point $(1)$ is \begin{equation} \label{Eq:II:6:7} \phi(1)=\int\frac{\rho(2)\,dV_2}{4\pi\epsO r_{12}}, \end{equation} where $\rho(2)$ is the charge density, $dV_2$ is the volume element at point $(2)$, and $r_{12}$ is the distance between points $(1)$ and $(2)$. The solution of the differential equation (6.6) is reduced to an integration over space. The solution (6.7) should be especially noted, because there are many situations in physics that lead to equations like \begin{equation*} \nabla^2(\text{something})=(\text{something else}), \end{equation*} and Eq. (6.7) is a prototype of the solution for any of these problems.
The solution of electrostatic field problems is thus completely straightforward when the positions of all the charges are known. Let’s see how it works in a few examples.
6–2The electric dipole
First, take two point charges, $+q$ and $-q$, separated by the distance $d$. Let the $z$-axis go through the charges, and pick the origin halfway between, as shown in Fig. 6–1. Then, using (4.24), the potential from the two charges is given by \begin{align} \phi(x,y,z&)\notag\\ \label{Eq:II:6:8} &=\frac{1}{4\pi\epsO}\biggl[ \frac{q}{\sqrt{[z-(d/2)]^2+x^2+y^2}}+ \frac{-q}{\sqrt{[z+(d/2)]^2+x^2+y^2}} \biggr]. \end{align} We are not going to write out the formula for the electric field, but we can always calculate it once we have the potential. So we have solved the problem of two charges.
There is an important special case in which the two charges are very close together—which is to say that we are interested in the fields only at distances from the charges large in comparison with their separation. We call such a close pair of charges a dipole. Dipoles are very common.
A “dipole” antenna can often be approximated by two charges separated by a small distance—if we don’t ask about the field too close to the antenna. (We are usually interested in antennas with moving charges; then the equations of statics do not really apply, but for some purposes they are an adequate approximation.)
More important perhaps, are atomic dipoles. If there is an electric field in any material, the electrons and protons feel opposite forces and are displaced relative to each other. In a conductor, you remember, some of the electrons move to the surfaces, so that the field inside becomes zero. In an insulator the electrons cannot move very far; they are pulled back by the attraction of the nucleus. They do, however, shift a little bit. So although an atom, or molecule, remains neutral in an external electric field, there is a very tiny separation of its positive and negative charges and it becomes a microscopic dipole. If we are interested in the fields of these atomic dipoles in the neighborhood of ordinary-sized objects, we are normally dealing with distances large compared with the separations of the pairs of charges.
In some molecules the charges are somewhat separated even in the absence of external fields, because of the form of the molecule. In a water molecule, for example, there is a net negative charge on the oxygen atom and a net positive charge on each of the two hydrogen atoms, which are not placed symmetrically but as in Fig. 6–2. Although the charge of the whole molecule is zero, there is a charge distribution with a little more negative charge on one side and a little more positive charge on the other. This arrangement is certainly not as simple as two point charges, but when seen from far away the system acts like a dipole. As we shall see a little later, the field at large distances is not sensitive to the fine details.
Let’s look, then, at the field of two opposite charges with a small separation $d$. If $d$ becomes zero, the two charges are on top of each other, the two potentials cancel, and there is no field. But if they are not exactly on top of each other, we can get a good approximation to the potential by expanding the terms of (6.8) in a power series in the small quantity $d$ (using the binomial expansion). Keeping terms only to first order in $d$, we can write \begin{equation*} \biggl(z-\frac{d}{2}\biggr)^2\approx z^2-zd. \end{equation*} It is convenient to write \begin{equation*} x^2+y^2+z^2=r^2. \end{equation*} Then \begin{equation*} \biggl(z-\frac{d}{2}\biggr)^2+x^2+y^2\approx r^2-zd= r^2\biggl(1-\frac{zd}{r^2}\biggr), \end{equation*} and \begin{equation*} \frac{1}{\sqrt{[z-(d/2)]^2+x^2+y^2}}\approx \frac{1}{\sqrt{r^2[1-(zd/r^2)]}}= \frac{1}{r}\biggl(1-\frac{zd}{r^2}\biggr)^{-1/2}. \end{equation*} Using the binomial expansion again for $[1-(zd/r^2)]^{-1/2}$—and throwing away terms with the square or higher powers of $d$—we get \begin{equation*} \frac{1}{r}\biggl(1+\frac{1}{2}\,\frac{zd}{r^2}\biggr). \end{equation*} Similarly, \begin{equation*} \frac{1}{\sqrt{[z+(d/2)]^2+x^2+y^2}}\approx \frac{1}{r}\biggl(1-\frac{1}{2}\,\frac{zd}{r^2}\biggr). \end{equation*} The difference of these two terms gives for the potential \begin{equation} \label{Eq:II:6:9} \phi(x,y,z)=\frac{1}{4\pi\epsO}\,\frac{z}{r^3}\,qd. \end{equation} The potential, and hence the field, which is its derivative, is proportional to $qd$, the product of the charge and the separation. This product is defined as the dipole moment of the two charges, for which we will use the symbol $p$ (do not confuse with momentum!): \begin{equation} \label{Eq:II:6:10} p=qd. \end{equation}
Equation (6.9) can also be written as \begin{equation} \label{Eq:II:6:11} \phi(x,y,z)=\frac{1}{4\pi\epsO}\,\frac{p\cos\theta}{r^2}, \end{equation} since $z/r=\cos\theta$, where $\theta$ is the angle between the axis of the dipole and the radius vector to the point $(x,y,z)$—see Fig. 6–1. The potential of a dipole decreases as $1/r^2$ for a given direction from the axis (whereas for a point charge it goes as $1/r$). The electric field $\FLPE$ of the dipole will then decrease as $1/r^3$.
We can put our formula into a vector form if we define $\FLPp$ as a
vector whose magnitude is $p$ and whose direction is along the axis of
the dipole, pointing from $-q$ toward $+q$. Then
\begin{equation}
\label{Eq:II:6:12}
p\cos\theta=\FLPp\cdot\FLPe_r,
\end{equation}
where $\FLPe_r$ is the unit radial vector (Fig. 6–3). We
can also represent the point $(x,y,z)$ by $\FLPr$. Then
Dipole potential:
\begin{equation}
\label{Eq:II:6:13}
\phi(\FLPr)=\frac{1}{4\pi\epsO}\,\frac{\FLPp\cdot\FLPe_r}{r^2}=
\frac{1}{4\pi\epsO}\,\frac{\FLPp\cdot\FLPr}{r^3}
\end{equation}
This formula is valid for a dipole with any orientation and position
if $\FLPr$ represents the vector from the dipole to the point of
interest.
If we want the electric field of the dipole we can get it by taking the gradient of $\phi$. For example, the $z$-component of the field is $-\ddpl{\phi}{z}$. For a dipole oriented along the $z$-axis we can use (6.9): \begin{equation} -\ddp{\phi}{z}=-\frac{p}{4\pi\epsO}\,\ddp{}{z}\biggl(\frac{z}{r^3}\biggr) =-\frac{p}{4\pi\epsO}\biggl(\frac{1}{r^3}-\frac{3z^2}{r^5}\biggr),\notag \end{equation} or \begin{equation} \label{Eq:II:6:14} E_z=\frac{p}{4\pi\epsO}\,\frac{3\cos^2\theta-1}{r^3}. \end{equation} The $x$- and $y$-components are \begin{equation*} E_x=\frac{p}{4\pi\epsO}\,\frac{3zx}{r^5},\quad E_y=\frac{p}{4\pi\epsO}\,\frac{3zy}{r^5}. \end{equation*} These two can be combined to give one component directed perpendicular to the $z$-axis, which we will call the transverse component $E_\perp$: \begin{equation} E_\perp=\sqrt{E_x^2+E_y^2}=\frac{p}{4\pi\epsO}\,\frac{3z}{r^5} \sqrt{x^2+y^2}\notag \end{equation} or \begin{equation} \label{Eq:II:6:15} E_\perp=\frac{p}{4\pi\epsO}\,\frac{3\cos\theta\sin\theta}{r^3}. \end{equation} The transverse component $E_\perp$ is in the $xy$-plane and points directly away from the axis of the dipole. The total field, of course, is \begin{equation*} E=\sqrt{E_z^2+E_\perp^2}. \end{equation*}
The dipole field varies inversely as the cube of the distance from the dipole. On the axis, at $\theta=0$, it is twice as strong as at $\theta=90^\circ$. At both of these special angles the electric field has only a $z$-component, but of opposite sign at the two places (Fig. 6–4).
6–3Remarks on vector equations
This is a good place to make a general remark about vector analysis. The fundamental proofs can be expressed by elegant equations in a general form, but in making various calculations and analyses it is always a good idea to choose the axes in some convenient way. Notice that when we were finding the potential of a dipole we chose the $z$-axis along the direction of the dipole, rather than at some arbitrary angle. This made the work much easier. But then we wrote the equations in vector form so that they would no longer depend on any particular coordinate system. After that, we are allowed to choose any coordinate system we wish, knowing that the relation is, in general, true. It clearly doesn’t make any sense to bother with an arbitrary coordinate system at some complicated angle when you can choose a neat system for the particular problem—provided that the result can finally be expressed as a vector equation. So by all means take advantage of the fact that vector equations are independent of any coordinate system.
On the other hand, if you are trying to calculate the divergence of a vector, instead of just looking at $\FLPdiv{\FLPE}$ and wondering what it is, don’t forget that it can always be spread out as \begin{equation*} \ddp{E_x}{x}+\ddp{E_y}{y}+\ddp{E_z}{z}. \end{equation*} If you can then work out the $x$-, $y$-, and $z$-components of the electric field and differentiate them, you will have the divergence. There often seems to be a feeling that there is something inelegant—some kind of defeat involved—in writing out the components; that somehow there ought always to be a way to do everything with the vector operators. There is often no advantage to it. The first time we encounter a particular kind of problem, it usually helps to write out the components to be sure we understand what is going on. There is nothing inelegant about putting numbers into equations, and nothing inelegant about substituting the derivatives for the fancy symbols. In fact, there is often a certain cleverness in doing just that. Of course when you publish a paper in a professional journal it will look better—and be more easily understood—if you can write everything in vector form. Besides, it saves print.
6–4The dipole potential as a gradient
We would like to point out a rather amusing thing about the dipole formula, Eq. (6.13). The potential can also be written as \begin{equation} \label{Eq:II:6:16} \phi=-\frac{1}{4\pi\epsO}\FLPp\cdot\FLPgrad{\biggl(\frac{1}{r}\biggr)}. \end{equation} If you calculate the gradient of $1/r$, you get \begin{equation*} \FLPgrad{\biggl(\frac{1}{r}\biggr)}=-\frac{\FLPr}{r^3}= -\frac{\FLPe_r}{r^2}, \end{equation*} and Eq. (6.16) is the same as Eq. (6.13).
How did we think of that? We just remembered that $\FLPe_r/r^2$ appeared in the formula for the field of a point charge, and that the field was the gradient of a potential which has a $1/r$ dependence.
There is a physical reason for being able to write the dipole potential in the form of Eq. (6.16). Suppose we have a point charge $q$ at the origin. The potential at the point $P$ at $(x,y,z)$ is \begin{equation*} \phi_0=\frac{q}{r}. \end{equation*} (Let’s leave off the $1/4\pi\epsO$ while we make these arguments; we can stick it in at the end.) Now if we move the charge $+q$ up a distance $\Delta z$, the potential at $P$ will change a little, by, say, $\Delta\phi_+$. How much is $\Delta\phi_+$? Well, it is just the amount that the potential would change if we were to leave the charge at the origin and move $P$ downward by the same distance $\Delta z$ (Fig. 6–5). That is, \begin{equation*} \Delta\phi_+=-\ddp{\phi_0}{z}\Delta z, \end{equation*} where by $\Delta z$ we mean the same as $d/2$. So, using $\phi_0=q/r$, we have that the potential from the positive charge is \begin{equation} \label{Eq:II:6:17} \phi_+=\frac{q}{r}-\ddp{}{z}\biggl(\frac{q}{r}\biggr)\frac{d}{2}. \end{equation}
Applying the same reasoning for the potential from the negative charge, we can write \begin{equation} \label{Eq:II:6:18} \phi_-=\frac{-q}{r}+\ddp{}{z}\biggl(\frac{-q}{r}\biggr)\frac{d}{2}. \end{equation} The total potential is the sum of (6.17) and (6.18): \begin{align} \label{Eq:II:6:19} \phi=\phi_++\phi_-&=-\ddp{}{z}\biggl(\frac{q}{r}\biggr)d\\[1ex] &=-\ddp{}{z}\biggl(\frac{1}{r}\biggr)qd\notag \end{align}
For other orientations of the dipole, we could represent the displacement of the positive charge by the vector $\Delta\FLPr_+$. We should then write the equation above Eq. (6.17) as \begin{equation*} \Delta\phi_+=-\FLPgrad{\phi_0}\cdot\Delta\FLPr_+, \end{equation*} where $\Delta\FLPr_+$ is then to be replaced by $\FLPd/2$. Completing the derivation as before, Eq. (6.19) would then become \begin{equation*} \phi=-\FLPgrad{\biggl(\frac{1}{r}\biggr)}\cdot q\FLPd. \end{equation*} This is the same as Eq. (6.16), if we replace $q\FLPd=\FLPp$, and put back the $1/4\pi\epsO$. Looking at it another way, we see that the dipole potential, Eq. (6.13), can be interpreted as \begin{equation} \label{Eq:II:6:20} \phi=-\FLPp\cdot\FLPgrad{\Phi_0}, \end{equation} where $\Phi_0=1/4\pi\epsO r$ is the potential of a unit point charge.
Although we can always find the potential of a known charge distribution by an integration, it is sometimes possible to save time by getting the answer with a clever trick. For example, one can often make use of the superposition principle. If we are given a charge distribution that can be made up of the sum of two distributions for which the potentials are already known, it is easy to find the desired potential by just adding the two known ones. One example of this is our derivation of (6.20), another is the following.
Suppose we have a spherical surface with a distribution of surface charge that varies as the cosine of the polar angle. The integration for this distribution is fairly messy. But, surprisingly, such a distribution can be analyzed by superposition. For imagine a sphere with a uniform volume density of positive charge, and another sphere with an equal uniform volume density of negative charge, originally superposed to make a neutral—that is, uncharged—sphere. If the positive sphere is then displaced slightly with respect to the negative sphere, the body of the uncharged sphere would remain neutral, but a little positive charge will appear on one side, and some negative charge will appear on the opposite side, as illustrated in Fig. 6–6. If the relative displacement of the two spheres is small, the net charge is equivalent to a surface charge (on a spherical surface), and the surface charge density will be proportional to the cosine of the polar angle.
Now if we want the potential from this distribution, we do not need to do an integral. We know that the potential from each of the spheres of charge is—for points outside the sphere—the same as from a point charge. The two displaced spheres are like two point charges; the potential is just that of a dipole.
In this way you can show that a charge distribution on a sphere of
radius $a$ with a surface charge density
\begin{equation*}
\sigma=\sigma_0\cos\theta
\end{equation*}
produces a field outside the sphere which is just that of a dipole
whose moment is
\begin{equation*}
p=\frac{4\pi\sigma_0 a^3}{3}.
\end{equation*}
It can also be shown that inside the sphere the field is constant,
with the value
\begin{equation*}
E=\frac{\sigma_0}{3\epsO}.
\end{equation*}
If $\theta$ is the angle from the positive $z$-axis, the electric
field inside the sphere is in the negative $z$-direction. The
example we have just considered is not as artificial as it may appear;
we will encounter it again in the theory of dielectrics.
2020.11.17: 1989년에는 그냥 얼렁뚱땅 넘어갔는데, 이번에 나름 이해한 것을 남긴다.
먼저
$ (e, b,c) \text{는 임의의 점, } x^2+y^2+(z-\frac{d}2)^2\leq a^2...(a), \,x^2+y^2+(z+\frac{d}2)^2\leq a^2...(b)
\\f(x, y,z)=\frac{(e-x, b-y, c-z)}{({(x-e)^{2}+(y-b)^{2}+(c-z)^2})^{\frac32}}, \,S(a)= x^2+y^2+z^2=a^2
\\
\text{라고 하고, ① (c)에 의한 ② (a)와 (b)의 superposition에 의한 전기장} E \text{ 를 계산한다.}
\\ \text{① (c)에 의한} \\
\text{간단한 계산에 의하여 (c)의 두께는 } d\cos{\phi}. \text{작은} d \text{에 대하여 뉴튼의 infinitesimally 잘게 쪼개는 방법을 적용하면, }
\\ \text{infinitesimal 조각의 전하= 면적소} (\Delta{A}) \times \text{높이} (d)
\times \text{전자밀도} ({\sigma_0} {\cos {\phi}})
\\E=
\frac{1}{4\pi{\epsilon_0}} \lim_{\Delta{A} \to 0}\sum_{x,y,z} \Delta{A(x,y,z)}d\sigma_0\cos{\phi}f(x,y,z)+O(d^2)(1, 1, 1)
\\=
\frac{d\sigma_0}{4\pi{\epsilon_0}}\int_{S(a)}\cos{\phi}f(x,y,z)dA + O(d^2)(1, 1, 1)....(**),
\\
\text{(**)의 첫항은 정확하게 전자 밀도 $σ_0\cos{ϕ}$인 구에서의 전기장 계산 적분에 곱하기 } d. \, O(d^2)|<=Kd^2, K \text{ 상수}
\\ \text{ ② (a)와 (b)의 superposition에 의한}
\\ \text{ (a)와(b)로부터 생기는 전기장은, 파인만II(5.7)에 의해, 각각}
\\
(\frac{\sigma_0 e}{3\epsilon_0}, \frac{\sigma_0 b}{3\epsilon_0}, \frac{\sigma_0(c-\frac{d}2)}{3\epsilon_0}),
-(\frac{\sigma_0 e}{3\epsilon_0}, \frac{\sigma_0 b}{3\epsilon_0}, \frac{\sigma_0(c+\frac{d}2)}{3\epsilon_0})
\\ \text{superposition 원리로 2개 벡터를 더하면,}
E=(0, 0, -\frac{\sigma_0{d}}{3\epsilon_0}),
\\
\text{ ③ ①= ②라고 놓고 양변을 } d \text{로 나누고 }
d → 0,
\\
\lim_{d\to 0}\frac{O(d^2)}d=0 \Rightarrow
\frac{\sigma_0}{4\pi{\epsilon_0}}\int_{S(a)}\cos{\phi}f(x,y,z)dA = (0, 0, -\frac{\sigma_0}{3\epsilon_0}), e^2+b^2+c^2\leq a^2$
위와 같은 방법으로 $p=\frac{4\pi\sigma_0 a^3}{3}$도 증명할 수 있다.
* 위 전기장을 적분으로 구한다는 것은 불가능. 보라, 특별한 경우의 계산을.
6–5The dipole approximation for an arbitrary distribution
The dipole field appears in another circumstance both interesting and important. Suppose that we have an object that has a complicated distribution of charge—like the water molecule (Fig. 6–2)—and we are interested only in the fields far away. We will show that it is possible to find a relatively simple expression for the fields which is appropriate for distances large compared with the size of the object.
We can think of our object as an assembly of point charges $q_i$ in a certain limited region, as shown in Fig. 6–7. (We can, later, replace $q_i$ by $\rho\,dV$ if we wish.) Let each charge $q_i$ be located at the displacement $\FLPd_i$ from an origin chosen somewhere in the middle of the group of charges. What is the potential at the point $P$, located at $\FLPR$, where $\FLPR$ is much larger than the maximum $\FLPd_i$? The potential from the whole collection is given by \begin{equation} \label{Eq:II:6:21} \phi=\frac{1}{4\pi\epsO}\sum_i\frac{q_i}{r_i}, \end{equation} where $r_i$ is the distance from $P$ to the charge $q_i$ (the length of the vector $\FLPR-\FLPd_i$). Now if the distance from the charges to $P$, the point of observation, is enormous, each of the $r_i$’s can be approximated by $R$. Each term becomes $q_i/R$, and we can take $1/R$ out as a factor in front of the summation. This gives us the simple result \begin{equation} \label{Eq:II:6:22} \phi=\frac{1}{4\pi\epsO}\,\frac{1}{R}\sum_iq_i= \frac{Q}{4\pi\epsO R}, \end{equation} where $Q$ is just the total charge of the whole object. Thus we find that for points far enough from any lump of charge, the lump looks like a point charge. The result is not too surprising.
But what if there are equal numbers of positive and negative charges? Then the total charge $Q$ of the object is zero. This is not an unusual case; in fact, as we know, objects are usually neutral. The water molecule is neutral, but the charges are not all at one point, so if we are close enough we should be able to see some effects of the separate charges. We need a better approximation than (6.22) for the potential from an arbitrary distribution of charge in a neutral object. Equation (6.21) is still precise, but we can no longer just set $r_i=R$. We need a more accurate expression for $r_i$. If the point $P$ is at a large distance, $r_i$ will differ from $R$ to an excellent approximation by the projection of $\FLPd$ on $\FLPR$, as can be seen from Fig. 6–7. (You should imagine that $P$ is really farther away than is shown in the figure.) In other words, if $\FLPe_R$ is the unit vector in the direction of $\FLPR$, then our next approximation to $r_i$ is \begin{equation} \label{Eq:II:6:23} r_i\approx R-\FLPd_i\cdot\FLPe_R. \end{equation} What we really want is $1/r_i$, which, since $d_i\ll R$, can be written to our approximation as \begin{equation} \label{Eq:II:6:24} \frac{1}{r_i}\approx\frac{1}{R}\biggl(1+\frac{\FLPd_i\cdot\FLPe_R}{R}\biggr). \end{equation} Substituting this in (6.21), we get that the potential is \begin{equation} \label{Eq:II:6:25} \phi=\frac{1}{4\pi\epsO}\biggl(\frac{Q}{R}+ \sum_iq_i\frac{\FLPd_i\cdot\FLPe_R}{R^2}+\dotsb\biggr). \end{equation} The three dots indicate the terms of higher order in $d_i/R$ that we have neglected. These, as well as the ones we have already obtained, are successive terms in a Taylor expansion of $1/r_i$ about $1/R$ in powers of $d_i/R$.
The first term in (6.25) is what we got before; it drops out if the object is neutral. The second term depends on $1/R^2$, just as for a dipole. In fact, if we define \begin{equation} \label{Eq:II:6:26} \FLPp=\sum_iq_i\FLPd_i \end{equation} as a property of the charge distribution, the second term of the potential (6.25) is \begin{equation} \label{Eq:II:6:27} \phi=\frac{1}{4\pi\epsO}\,\frac{\FLPp\cdot\FLPe_R}{R^2}, \end{equation} precisely a dipole potential. The quantity $\FLPp$ is called the dipole moment of the distribution. It is a generalization of our earlier definition, and reduces to it for the special case of two point charges.
Our result is that, far enough away from any mess of charges that is as a whole neutral, the potential is a dipole potential. It decreases as $1/R^2$ and varies as $\cos\theta$—and its strength depends on the dipole moment of the distribution of charge. It is for these reasons that dipole fields are important, since the simple case of a pair of point charges is quite rare.
The water molecule, for example, has a rather strong dipole moment. The electric fields that result from this moment are responsible for some of the important properties of water. For many molecules, for example CO$_2$, the dipole moment vanishes because of the symmetry of the molecule. For them we should expand still more accurately, obtaining another term in the potential which decreases as $1/R^3$, and which is called a quadrupole potential. We will discuss such cases later.
6–6The fields of charged conductors
We have now finished with the examples we wish to cover of situations in which the charge distribution is known from the start. It has been a problem without serious complications, involving at most some integrations. We turn now to an entirely new kind of problem, the determination of the fields near charged conductors.
Suppose that we have a situation in which a total charge $Q$ is placed on an arbitrary conductor. Now we will not be able to say exactly where the charges are. They will spread out in some way on the surface. How can we know how the charges have distributed themselves on the surface? They must distribute themselves so that the potential of the surface is constant. If the surface were not an equipotential, there would be an electric field inside the conductor, and the charges would keep moving until it became zero. The general problem of this kind can be solved in the following way. We guess at a distribution of charge and calculate the potential. If the potential turns out to be constant everywhere on the surface, the problem is finished. If the surface is not an equipotential, we have guessed the wrong distribution of charges, and should guess again—hopefully with an improved guess! This can go on forever, unless we are judicious about the successive guesses.
The question of how to guess at the distribution is mathematically difficult. Nature, of course, has time to do it; the charges push and pull until they all balance themselves. When we try to solve the problem, however, it takes us so long to make each trial that that method is very tedious. With an arbitrary group of conductors and charges the problem can be very complicated, and in general it cannot be solved without rather elaborate numerical methods. Such numerical computations, these days, are set up on a computing machine that will do the work for us, once we have told it how to proceed.
On the other hand, there are a lot of little practical cases where it would be nice to be able to find the answer by some more direct method—without having to write a program for a computer. Fortunately, there are a number of cases where the answer can be obtained by squeezing it out of Nature by some trick or other. The first trick we will describe involves making use of solutions we have already obtained for situations in which charges have specified locations.
6–7The method of images
We have solved, for example, the field of two point charges. Figure 6–8 shows some of the field lines and equipotential surfaces we obtained by the computations in Chapter 4. Now consider the equipotential surface marked $A$. Suppose we were to shape a thin sheet of metal so that it just fits this surface. If we place it right at the surface and adjust its potential to the proper value, no one would ever know it was there, because nothing would be changed.
But notice! We have really solved a new problem. We have a situation in which the surface of a curved conductor with a given potential is placed near a point charge. If the metal sheet we placed at the equipotential surface eventually closes on itself (or, in practice, if it goes far enough) we have the kind of situation considered in Section 5–10, in which our space is divided into two regions, one inside and one outside a closed conducting shell. We found there that the fields in the two regions are quite independent of each other. So we would have the same fields outside our curved conductor no matter what is inside. We can even fill up the whole inside with conducting material.
2025.3.27: 전자는 기를 내뿜는 호스 같은 거. equipotential이란 건 전자로부터의 기들이 채워져 외부로부터의 기들과 평형을 유지한다는 거.
따라서 빈 곳을 전도체로 채우면 그 안의 전자들로부터 나오는 기들이 외부와 평형 이를 만큼의 기를 내뿜으로써 euipotential 유지
3.28: 작용 반작용 법칙은 질량 사이의 충돌은 벽에 균열 만들고, 그 찰나 순간에 기들 교류, 즉 같은 양(?)의 기들이 자리 바꿈한다는 것. 그 결과 운동량 보존.
6.28: 음양 전하의 밀당, 만만한 곳으로 치고 나가는 기질: 내뿜기 위해서 적은, 뒤집으면, 빨아들이기 위해서는 기가 많은 쪽을 찾는 그 기질
1. 전자는 기를 내뿜으며 밀어내는 다른 전자 근처에는 기들이 많으니 멀리하고
(1) pusing momentum, (2) 에너지와 모멘텀 밀도는 상수 배 차이
2. 그 반면에 양전하/hole은 기들이 많이 모인 곳으로 간다, 빨아들이기 위해. 빨아들이는 것들 주변에 기들이 상대적으로 적으니 피할 수 밖에.
3. 부호가 다른 전하들은 한쪽은 내뿜고 다른쪽은 흡입하니 서로 가까이 하는 거.
7.19: 질량의 끌림, 소위 만류인력은 지퍼 움직임과 비슷. 스테디 플로우 기들이 뭉치는 형태를 hole의 흡입으로 생각하면 차이점은 기 공급 소스가(지퍼) 있기에 그곳으로 몰리는 것으로 볼 수 있다
9.15: backward thinking: 회전 skrew 전진의 역 .... 떨어져 내리는 물에 spiral helix up
12.3: 입자들 간의 밀당
2025.1.7: 물질은 기들 구조물로 핵심은 벽(경계, boundary)... 그 형성 근거들
1. 2 영역의 경계
2. no matter what is inside, 든 생각: 물질 형성하는 steady flow 기들이 확실한 경계를 지키는 이유 - 1.1
3. image idea works just as -1.5
4. 기 밀도
Thus we can compute the fields in Fig. 6–9 by computing the field due to $q$ and to an imaginary point charge $-q$ at a suitable point. The point charge we “imagine” existing behind the conducting surface is called an image charge.
In books you can find long lists of solutions for hyperbolic-shaped conductors and other complicated looking things, and you wonder how anyone ever solved these terrible shapes. They were solved backwards! Someone solved a simple problem with given charges. He then saw that some equipotential surface showed up in a new shape, and he wrote a paper in which he pointed out that the field outside that particular shape can be described in a certain way.
6–8A point charge near a conducting plane
As the simplest application of the use of this method, let’s make use of the plane equipotential surface $B$ of Fig. 6–8. With it, we can solve the problem of a charge in front of a conducting sheet. We just cross out the left-hand half of the picture. The field lines for our solution are shown in Fig. 6–10. Notice that the plane, since it was halfway between the two charges, has zero potential. We have solved the problem of a positive charge next to a grounded conducting sheet.
We have now solved for the total field, but what about the real charges that are responsible for it? There are, in addition to our positive point charge, some induced negative charges on the conducting sheet that have been attracted by the positive charge (from large distances away). Now suppose that for some technical reason—or out of curiosity—you would like to know how the negative charges are distributed on the surface. You can find the surface charge density by using the result we worked out in Section 5–9 with Gauss’ law. The normal component of the electric field just outside a conductor is equal to the density of surface charge $\sigma$ divided by $\epsO$. We can obtain the density of charge at any point on the surface by working backwards from the normal component of the electric field at the surface. We know that, because we know the field everywhere.
Consider a point on the surface at the distance $\rho$ from the point directly beneath the positive charge (Fig. 6–10). The electric field at this point is normal to the surface and is directed into it. The component normal to the surface of the field from the positive point charge is \begin{equation} \label{Eq:II:6:28} E_{n+}=-\frac{1}{4\pi\epsO}\,\frac{aq}{(a^2+\rho^2)^{3/2}}. \end{equation} To this we must add the electric field produced by the negative image charge. That just doubles the normal component (and cancels all others), so the charge density $\sigma$ at any point on the surface is \begin{equation} \label{Eq:II:6:29} \sigma(\rho)=\epsO E(\rho)=-\frac{2aq}{4\pi(a^2+\rho^2)^{3/2}}. \end{equation}
An interesting check on our work is to integrate $\sigma$ over the whole surface. We find that the total induced charge is $-q$, as it should be.
One further question: Is there a force on the point charge? Yes, because there is an attraction from the induced negative surface charge on the plate. Now that we know what the surface charges are (from Eq. 6.29), we could compute the force on our positive point charge by an integral. But we also know that the force acting on the positive charge is exactly the same as it would be with the negative image charge instead of the plate, because the fields in the neighborhood are the same in both cases. The point charge feels a force toward the plate whose magnitude is \begin{equation} \label{Eq:II:6:30} F=\frac{1}{4\pi\epsO}\,\frac{q^2}{(2a)^2}. \end{equation} We have found the force much more easily than by integrating over all the negative charges.
6–9A point charge near a conducting sphere
What other surfaces besides a plane have a simple solution? The next most simple shape is a sphere. Let’s find the fields around a grounded metal sphere which has a point charge $q$ near it, as shown in Fig. 6–11. Now we must look for a simple physical situation which gives a sphere for an equipotential surface. If we look around at problems people have already solved, we find that someone has noticed that the field of two unequal point charges has an equipotential that is a sphere. Aha! If we choose the location of an image charge—and pick the right amount of charge—maybe we can make the equipotential surface fit our sphere. Indeed, it can be done with the following prescription.
Assume that you want the equipotential surface to be a sphere of radius $a$ with its center at the distance $b$ from the charge $q$. Put an image charge of strength $q'=-q(a/b)$ on the line from the charge to the center of the sphere, and at a distance $a^2/b$ from the center. The sphere will be at zero potential.
The mathematical reason stems from the fact that a sphere is the locus of all points for which the distances from two points are in a constant ratio. Referring to Fig. 6–11, the potential at $P$ from $q$ and $q'$ is proportional to \begin{equation*} \frac{q}{r_1}+\frac{q'}{r_2}. \end{equation*} The potential will thus be zero at all points for which \begin{equation*} \frac{q'}{r_2}=-\frac{q}{r_1}\quad\text{or}\quad \frac{r_2}{r_1}=-\frac{q'}{q}. \end{equation*} If we place $q'$ at the distance $a^2/b$ from the center, the ratio $r_2/r_1$ has the constant value $a/b$. Then if \begin{equation} \label{Eq:II:6:31} \frac{q'}{q}=-\frac{a}{b} \end{equation} the sphere is an equipotential. Its potential is, in fact, zero.
What happens if we are interested in a sphere that is not at zero potential? That would be so only if its total charge happens accidentally to be $q'$. Of course if it is grounded, the charges induced on it would have to be just that. But what if it is insulated, and we have put no charge on it? Or if we know that the total charge $Q$ has been put on it? Or just that it has a given potential not equal to zero? All these questions are easily answered. We can always add a point charge $q''$ at the center of the sphere. The sphere still remains an equipotential by superposition; only the magnitude of the potential will be changed.
If we have, for example, a conducting sphere which is initially uncharged and insulated from everything else, and we bring near to it the positive point charge $q$, the total charge of the sphere will remain zero. The solution is found by using an image charge $q'$ as before, but, in addition, adding a charge $q''$ at the center of the sphere, choosing \begin{equation} \label{Eq:II:6:32} q''=-q'=\frac{a}{b}\,q. \end{equation} The fields everywhere outside the sphere are given by the superposition of the fields of $q$, $q'$, and $q''$. The problem is solved.
We can see now that there will be a force of attraction between the sphere and the point charge $q$. It is not zero even though there is no charge on the neutral sphere. Where does the attraction come from? When you bring a positive charge up to a conducting sphere, the positive charge attracts negative charges to the side closer to itself and leaves positive charges on the surface of the far side. The attraction by the negative charges exceeds the repulsion from the positive charges; there is a net attraction. We can find out how large the attraction is by computing the force on $q$ in the field produced by $q'$ and $q''$. The total force is the sum of the attractive force between $q$ and a charge $q'=-(a/b)q$, at the distance $b-(a^2/b)$, and the repulsive force between $q$ and a charge $q''=+(a/b)q$ at the distance $b$.
Those who were entertained in childhood by the baking powder box which has on its label a picture of a baking powder box which has on its label a picture of a baking powder box which has … may be interested in the following problem. Two equal spheres, one with a total charge of $+Q$ and the other with a total charge of $-Q$, are placed at some distance from each other. What is the force between them? The problem can be solved with an infinite number of images. One first approximates each sphere by a charge at its center. These charges will have image charges in the other sphere. The image charges will have images, etc., etc., etc. The solution is like the picture on the box of baking powder—and it converges pretty fast.
6–10Condensers; parallel plates
We take up now another kind of a problem involving conductors. Consider two large metal plates which are parallel to each other and separated by a distance small compared with their width. Let’s suppose that equal and opposite charges have been put on the plates. The charges on each plate will be attracted by the charges on the other plate, and the charges will spread out uniformly on the inner surfaces of the plates. The plates will have surface charge densities $+\sigma$ and $-\sigma$, respectively, as in Fig. 6–12. From Chapter 5 we know that the field between the plates is $\sigma/\epsO$, and that the field outside the plates is zero. The plates will have different potentials $\phi_1$ and $\phi_2$. For convenience we will call the difference $V$; it is often called the “voltage”: \begin{equation*} \phi_1-\phi_2=V. \end{equation*} (You will find that sometimes people use $V$ for the potential, but we have chosen to use $\phi$.)
The potential difference $V$ is the work per unit charge required to carry a small charge from one plate to the other, so that \begin{equation} \label{Eq:II:6:33} V=Ed=\frac{\sigma}{\epsO}\,d=\frac{d}{\epsO A}\,Q, \end{equation} where $\pm Q$ is the total charge on each plate, $A$ is the area of the plates, and $d$ is the separation.
We find that the voltage is proportional to the charge. Such a proportionality between $V$ and $Q$ is found for any two conductors in space if there is a plus charge on one and an equal minus charge on the other. The potential difference between them—that is, the voltage—will be proportional to the charge. (We are assuming that there are no other charges around.)
Why this proportionality? Just the superposition principle. Suppose we know the solution for one set of charges, and then we superimpose two such solutions. The charges are doubled, the fields are doubled, and the work done in carrying a unit charge from one point to the other is also doubled. Therefore the potential difference between any two points is proportional to the charges. In particular, the potential difference between the two conductors is proportional to the charges on them. Someone originally wrote the equation of proportionality the other way. That is, they wrote \begin{equation*} Q=CV, \end{equation*} where $C$ is a constant. This coefficient of proportionality is called the capacity, and such a system of two conductors is called a condenser.1 For our parallel-plate condenser \begin{equation} \label{Eq:II:6:34} C=\frac{\epsO A}{d}\quad(\text{parallel plates}). \end{equation}
This formula is not exact, because the field is not really uniform everywhere between the plates, as we assumed. The field does not just suddenly quit at the edges, but really is more as shown in Fig. 6–13. The total charge is not $\sigma A$, as we have assumed—there is a little correction for the effects at the edges. To find out what the correction is, we will have to calculate the field more exactly and find out just what does happen at the edges. That is a complicated mathematical problem which can, however, be solved by techniques which we will not describe now. The result of such calculations is that the charge density rises somewhat near the edges of the plates. This means that the capacity of the plates is a little higher than we computed.
We have talked about the capacity for two conductors only. Sometimes people talk about the capacity of a single object. They say, for instance, that the capacity of a sphere of radius $a$ is $4\pi\epsO a$. What they imagine is that the other terminal is another sphere of infinite radius—that when there is a charge $+Q$ on the sphere, the opposite charge, $-Q$, is on an infinite sphere. One can also speak of capacities when there are three or more conductors, a discussion we shall, however, defer.
Suppose that we wish to have a condenser with a very large capacity. We could get a large capacity by taking a very big area and a very small separation. We could put waxed paper between sheets of aluminum foil and roll it up. (If we seal it in plastic, we have a typical radio-type condenser.) What good is it? It is good for storing charge. If we try to store charge on a ball, for example, its potential rises rapidly as we charge it up. It may even get so high that the charge begins to escape into the air by way of sparks. But if we put the same charge on a condenser whose capacity is very large, the voltage developed across the condenser will be small.
In many applications in electronic circuits, it is useful to have something which can absorb or deliver large quantities of charge without changing its potential much. A condenser (or “capacitor”) does just that. There are also many applications in electronic instruments and in computers where a condenser is used to get a specified change in voltage in response to a particular change in charge. We have seen a similar application in Chapter 23, Vol. I, where we described the properties of resonant circuits.
From the definition of $C$, we see that its unit is one coulomb/volt. This unit is also called a farad. Looking at Eq. (6.34), we see that one can express the units of $\epsO$ as farad/meter, which is the unit most commonly used. Typical sizes of condensers run from one micro-microfarad ($1$ picofarad) to millifarads. Small condensers of a few picofarads are used in high-frequency tuned circuits, and capacities up to hundreds or thousands of microfarads are found in power-supply filters. A pair of plates one square centimeter in area with a one millimeter separation have a capacity of roughly one micro-microfarad.
6–11High-voltage breakdown
We would like now to discuss qualitatively some of the characteristics of the fields around conductors. If we charge a conductor that is not a sphere, but one that has on it a point or a very sharp end, as, for example, the object sketched in Fig. 6–14, the field around the point is much higher than the field in the other regions. The reason is, qualitatively, that charges try to spread out as much as possible on the surface of a conductor, and the tip of a sharp point is as far away as it is possible to be from most of the surface. Some of the charges on the plate get pushed all the way to the tip. A relatively small amount of charge on the tip can still provide a large surface density; a high charge density means a high field just outside.
One way to see that the field is highest at those places on a conductor where the radius of curvature is smallest is to consider the combination of a big sphere and a little sphere connected by a wire, as shown in Fig. 6–15. It is a somewhat idealized version of the conductor of Fig. 6–14. The wire will have little influence on the fields outside; it is there to keep the spheres at the same potential. Now, which ball has the biggest field at its surface? If the ball on the left has the radius $a$ and carries a charge $Q$, its potential is about \begin{equation*} \phi_1=\frac{1}{4\pi\epsO}\,\frac{Q}{a}. \end{equation*} (Of course the presence of one ball changes the charge distribution on the other, so that the charges are not really spherically symmetric on either. But if we are interested only in an estimate of the fields, we can use the potential of a spherical charge.) If the smaller ball, whose radius is $b$, carries the charge $q$, its potential is about \begin{equation*} \phi_2=\frac{1}{4\pi\epsO}\,\frac{q}{b}. \end{equation*} But $\phi_1=\phi_2$, so \begin{equation*} \frac{Q}{a}=\frac{q}{b}. \end{equation*} On the other hand, the field at the surface (see Eq. 5.8) is proportional to the surface charge density, which is like the total charge over the radius squared. We get that \begin{equation} \label{Eq:II:6:35} \frac{E_a}{E_b}=\frac{Q/a^2}{q/b^2}=\frac{b}{a}. \end{equation} Therefore the field is higher at the surface of the small sphere. The fields are in the inverse proportion of the radii.
This result is technically very important, because air will break down if the electric field is too great. What happens is that a loose charge (electron, or ion) somewhere in the air is accelerated by the field, and if the field is very great, the charge can pick up enough speed before it hits another atom to be able to knock an electron off that atom. As a result, more and more ions are produced. Their motion constitutes a discharge, or spark. If you want to charge an object to a high potential and not have it discharge itself by sparks in the air, you must be sure that the surface is smooth, so that there is no place where the field is abnormally large.
6–12The field-emission microscope
There is an interesting application of the extremely high electric field which surrounds any sharp protuberance on a charged conductor. The field-emission microscope depends for its operation on the high fields produced at a sharp metal point.2 It is built in the following way. A very fine needle, with a tip whose diameter is about $1000$ angstroms, is placed at the center of an evacuated glass sphere (Fig. 6–16). The inner surface of the sphere is coated with a thin conducting layer of fluorescent material, and a very high potential difference is applied between the fluorescent coating and the needle.
Let’s first consider what happens when the needle is negative with respect to the fluorescent coating. The field lines are highly concentrated at the sharp point. The electric field can be as high as $40$ million volts per centimeter. In such intense fields, electrons are pulled out of the surface of the needle and accelerated across the potential difference between the needle and the fluorescent layer. When they arrive there they cause light to be emitted, just as in a television picture tube.
The electrons which arrive at a given point on the fluorescent surface are, to an excellent approximation, those which leave the other end of the radial field line, because the electrons will travel along the field line passing from the point to the surface. Thus we see on the surface some kind of an image of the tip of the needle. More precisely, we see a picture of the emissivity of the surface of the needle—that is the ease with which electrons can leave the surface of the metal tip. If the resolution were high enough, one could hope to resolve the positions of the individual atoms on the tip of the needle. With electrons, this resolution is not possible for the following reasons. First, there is quantum-mechanical diffraction of the electron waves which blurs the image. Second, due to the internal motions of the electrons in the metal they have a small sideways initial velocity when they leave the needle, and this random transverse component of the velocity causes some smearing of the image. The combination of these two effects limits the resolution to $25$ Å or so.
If, however, we reverse the polarity and introduce a small amount of helium gas into the bulb, much higher resolutions are possible. When a helium atom collides with the tip of the needle, the intense field there strips an electron off the helium atom, leaving it positively charged. The helium ion is then accelerated outward along a field line to the fluorescent screen. Since the helium ion is so much heavier than an electron, the quantum-mechanical wavelengths are much smaller. If the temperature is not too high, the effect of the thermal velocities is also smaller than in the electron case. With less smearing of the image a much sharper picture of the point is obtained. It has been possible to obtain magnifications up to $2{,}000{,}000$ times with the positive ion field-emission microscope—a magnification ten times better than is obtained with the best electron microscope.

Figure 6–17 is an example of the results which were obtained with a field-ion microscope, using a tungsten needle. The center of a tungsten atom ionizes a helium atom at a slightly different rate than the spaces between the tungsten atoms. The pattern of spots on the fluorescent screen shows the arrangement of the individual atoms on the tungsten tip. The reason the spots appear in rings can be understood by visualizing a large box of balls packed in a rectangular array, representing the atoms in the metal. If you cut an approximately spherical section out of this box, you will see the ring pattern characteristic of the atomic structure. The field-ion microscope provided human beings with the means of seeing atoms for the first time. This is a remarkable achievement, considering the simplicity of the instrument.
- Some people think the words “capacitance” and “capacitor” should be used, instead of “capacity” and “condensor.” We have decided to use the older terminology, because it is still more commonly heard in the physics laboratory—even if not in textbooks! ↩
- See E. W. Müller: “The field-ion microscope,” Advances in Electronics and Electron Physics, 13, 83–179 (1960). Academic Press, New York. ↩