35 Paramagnetism and Magnetic Resonance
Paramagnetism and Magnetic Resonance
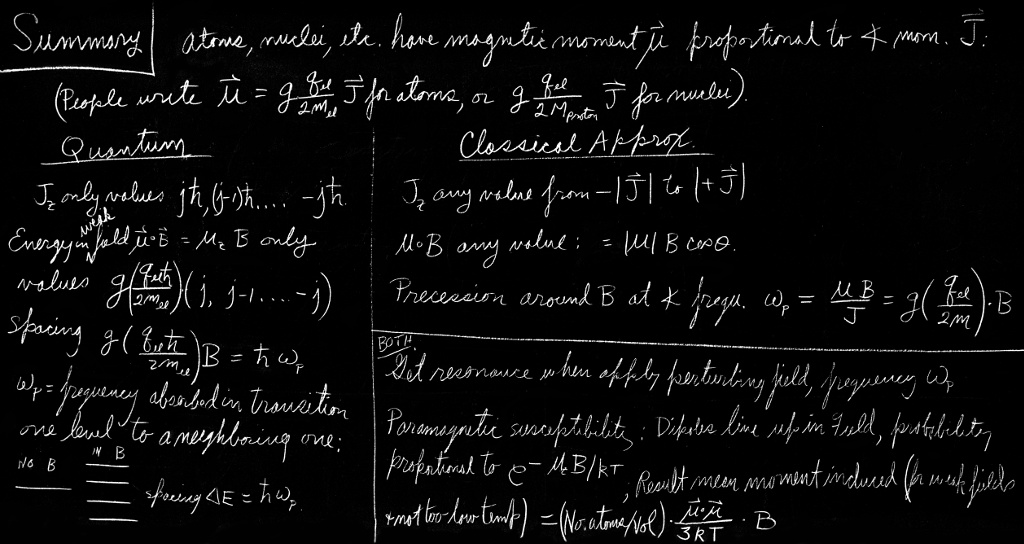
| Review: | Chapter 11, Inside Dielectrics |
35–1Quantized magnetic states
In the last chapter we described how in quantum mechanics the angular momentum of a thing does not have an arbitrary direction, but its component along a given axis can take on only certain equally spaced, discrete values. It is a shocking and peculiar thing. You may think that perhaps we should not go into such things until your minds are more advanced and ready to accept this kind of an idea. Actually, your minds will never become more advanced—in the sense of being able to accept such a thing easily. There isn’t any descriptive way of making it intelligible that isn’t so subtle and advanced in its own form that it is more complicated than the thing you were trying to explain. The behavior of matter on a small scale—as we have remarked many times—is different from anything that you are used to and is very strange indeed. As we proceed with classical physics, it is a good idea to try to get a growing acquaintance with the behavior of things on a small scale, at first as a kind of experience without any deep understanding. Understanding of these matters comes very slowly, if at all. Of course, one does get better able to know what is going to happen in a quantum-mechanical situation—if that is what understanding means—but one never gets a comfortable feeling that these quantum-mechanical rules are “natural.” Of course they are, but they are not natural to our own experience at an ordinary level. We should explain that the attitude that we are going to take with regard to this rule about angular momentum is quite different from many of the other things we have talked about. We are not going to try to “explain” it, but we must at least tell you what happens; it would be dishonest to describe the magnetic properties of materials without mentioning the fact that the classical description of magnetism—of angular momentum and magnetic moments—is incorrect.
One of the most shocking and disturbing features about quantum mechanics is that if you take the angular momentum along any particular axis you find that it is always an integer or half-integer times $\hbar$. This is so no matter which axis you take. The subtleties involved in that curious fact—that you can take any other axis and find that the component for it is also locked to the same set of values—we will leave to a later chapter, when you will experience the delight of seeing how this apparent paradox is ultimately resolved.
We will now just accept the fact that for every atomic system there is a number $j$, called the spin of the system—which must be an integer or a half-integer—and that the component of the angular momentum along any particular axis will always have one of the following values between $+j\hbar$ and $-j\hbar$: \begin{equation} \label{Eq:II:35:1} J_z=\text{one of}\, \left\{ \begin{array}{@{}l@{}} \phantom{-}j\\ \phantom{-}j-1\\ \phantom{-}j-2\\ \phantom{-j}\:\:\vdots\\ -j+2\\ -j+1\\ -j \end{array} \right\} \cdot\hbar. \end{equation}
We have also mentioned that every simple atomic system has a magnetic moment which has the same direction as the angular momentum. This is true not only for atoms and nuclei but also for the fundamental particles. Each fundamental particle has its own characteristic value of $j$ and its magnetic moment. (For some particles, both are zero.) What we mean by “the magnetic moment” in this statement is that the energy of the system in a magnetic field, say in the $z$-direction, can be written as $-\mu_zB$ for small magnetic fields. We must have the condition that the field should not be too great, otherwise it could disturb the internal motions of the system and the energy would not be a measure of the magnetic moment that was there before the field was turned on. But if the field is sufficiently weak, the field changes the energy by the amount \begin{equation} \label{Eq:II:35:2} \Delta U=-\mu_zB, \end{equation} with the understanding that in this equation we are to replace $\mu_z$ by \begin{equation} \label{Eq:II:35:3} \mu_z=g\biggl(\frac{q}{2m}\biggr)J_z, \end{equation} where $J_z$ has one of the values in Eq. (35.1).
Suppose we take a system with a spin $j=3/2$. Without a magnetic field, the system has four different possible states corresponding to the different values of $J_z$, all of which have exactly the same energy. But the moment we turn on the magnetic field, there is an additional energy of interaction which separates these states into four slightly different energy levels. The energies of these levels are given by a certain energy proportional to $B$, multiplied by $\hbar$ times $3/2$, $1/2$, $-1/2$, and $-3/2$—the values of $J_z$. The splitting of the energy levels for atomic systems with spins of $1/2$, $1$, and $3/2$ are shown in the diagrams of Fig. 35-1. (Remember that for any arrangement of electrons the magnetic moment is always directed opposite to the angular momentum.)
You will notice from the diagrams that the “center of gravity” of the energy levels is the same with and without a magnetic field. Also notice that the spacings from one level to the next are always equal for a given particle in a given magnetic field. We are going to write the energy spacing, for a given magnetic field $B$, as $\hbar\omega_p$—which is just a definition of $\omega_p$. Using Eqs. (35.2) and (35.3), we have \begin{equation*} \hbar\omega_p=g\,\frac{q}{2m}\,\hbar B \end{equation*} or \begin{equation} \label{Eq:II:35:4} \phantom{\hbar}\omega_p=g\,\frac{q}{2m}\,B. \end{equation} The quantity $g(q/2m)$ is just the ratio of the magnetic moment to the angular momentum—it is a property of the particle. Equation (35.4) is the same formula that we got in Chapter 34 for the angular velocity of precession in a magnetic field, for a gyroscope whose angular momentum is $\FLPJ$ and whose magnetic moment is $\FLPmu$.
35–2The Stern-Gerlach experiment
The fact that the angular momentum is quantized is such a surprising thing that we will talk a little bit about it historically. It was a shock from the moment it was discovered (although it was expected theoretically). It was first observed in an experiment done in 1922 by Stern and Gerlach. If you wish, you can consider the experiment of Stern-Gerlach as a direct justification for a belief in the quantization of angular momentum. Stern and Gerlach devised an experiment for measuring the magnetic moment of individual silver atoms. They produced a beam of silver atoms by evaporating silver in a hot oven and letting some of them come out through a series of small holes. This beam was directed between the pole tips of a special magnet, as shown in Fig. 35-2. Their idea was the following. If the silver atom has a magnetic moment $\FLPmu$, then in a magnetic field $\FLPB$ it has an energy $-\mu_zB$, where $z$ is the direction of the magnetic field. In the classical theory, $\mu_z$ would be equal to the magnetic moment times the cosine of the angle between the moment and the magnetic field, so the extra energy in the field would be \begin{equation} \label{Eq:II:35:5} \Delta U=-\mu B\cos\theta. \end{equation} Of course, as the atoms come out of the oven, their magnetic moments would point in every possible direction, so there would be all values of $\theta$. Now if the magnetic field varies very rapidly with $z$—if there is a strong field gradient—then the magnetic energy will also vary with position, and there will be a force on the magnetic moments whose direction will depend on whether cosine $\theta$ is positive or negative. The atoms will be pulled up or down by a force proportional to the derivative of the magnetic energy; from the principle of virtual work, \begin{equation} \label{Eq:II:35:6} F_z=-\ddp{U}{z}=\mu\cos\theta\,\ddp{B}{z}. \end{equation}
Stern and Gerlach made their magnet with a very sharp edge on one of the pole tips in order to produce a very rapid variation of the magnetic field. The beam of silver atoms was directed right along this sharp edge, so that the atoms would feel a vertical force in the inhomogeneous field. A silver atom with its magnetic moment directed horizontally would have no force on it and would go straight past the magnet. An atom whose magnetic moment was exactly vertical would have a force pulling it up toward the sharp edge of the magnet. An atom whose magnetic moment was pointed downward would feel a downward push. Thus, as they left the magnet, the atoms would be spread out according to their vertical components of magnetic moment. In the classical theory all angles are possible, so that when the silver atoms are collected by deposition on a glass plate, one should expect a smear of silver along a vertical line. The height of the line would be proportional to the magnitude of the magnetic moment. The abject failure of classical ideas was completely revealed when Stern and Gerlach saw what actually happened. They found on the glass plate two distinct spots. The silver atoms had formed two beams.
That a beam of atoms whose spins would apparently be randomly oriented gets split up into two separate beams is most miraculous. How does the magnetic moment know that it is only allowed to take on certain components in the direction of the magnetic field? Well, that was really the beginning of the discovery of the quantization of angular momentum, and instead of trying to give you a theoretical explanation, we will just say that you are stuck with the result of this experiment just as the physicists of that day had to accept the result when the experiment was done. It is an experimental fact that the energy of an atom in a magnetic field takes on a series of individual values. For each of these values the energy is proportional to the field strength. So in a region where the field varies, the principle of virtual work tells us that the possible magnetic force on the atoms will have a set of separate values; the force is different for each state, so the beam of atoms is split into a small number of separate beams. From a measurement of the deflection of the beams, one can find the strength of the magnetic moment.
35–3The Rabi molecular-beam method
We would now like to describe an improved apparatus for the measurement of magnetic moments which was developed by I. I. Rabi and his collaborators. In the Stern-Gerlach experiment the deflection of atoms is very small, and the measurement of the magnetic moment is not very precise. Rabi’s technique permits a fantastic precision in the measurement of the magnetic moments. The method is based on the fact that the original energy of the atoms in a magnetic field is split up into a finite number of energy levels. That the energy of an atom in the magnetic field can have only certain discrete energies is really not more surprising than the fact that atoms in general have only certain discrete energy levels—something we mentioned often in Volume I. Why should the same thing not hold for atoms in a magnetic field? It does. But it is the attempt to correlate this with the idea of an oriented magnetic moment that brings out some of the strange implications of quantum mechanics.
When an atom has two levels which differ in energy by the amount $\Delta U$, it can make a transition from the upper level to the lower level by emitting a light quantum of frequency $\omega$, where \begin{equation} \label{Eq:II:35:7} \hbar\omega=\Delta U. \end{equation} The same thing can happen with atoms in a magnetic field. Only then, the energy differences are so small that the frequency does not correspond to light, but to microwaves or to radiofrequencies. The transitions from the lower energy level to an upper energy level of an atom can also take place with the absorption of light or, in the case of atoms in a magnetic field, by the absorption of microwave energy. Thus if we have an atom in a magnetic field, we can cause transitions from one state to another by applying an additional electromagnetic field of the proper frequency. In other words, if we have an atom in a strong magnetic field and we “tickle” the atom with a weak varying electromagnetic field, there will be a certain probability of knocking it to another level if the frequency is near to the $\omega$ in Eq. (35.7). For an atom in a magnetic field, this frequency is just what we have earlier called $\omega_p$ and it is given in terms of the magnetic field by Eq. (35.4). If the atom is tickled with the wrong frequency, the chance of causing a transition is very small. Thus there is a sharp resonance at $\omega_p$ in the probability of causing a transition. By measuring the frequency of this resonance in a known magnetic field $B$, we can measure the quantity $g(q/2m)$—and hence the $g$-factor—with great precision.
It is interesting that one comes to the same conclusion from a classical point of view. According to the classical picture, when we place a small gyroscope with a magnetic moment $\mu$ and an angular momentum $J$ in an external magnetic field, the gyroscope will precess about an axis parallel to the magnetic field. (See Fig. 35-3.) Suppose we ask: How can we change the angle of the classical gyroscope with respect to the field—namely, with respect to the $z$-axis? The magnetic field produces a torque around a horizontal axis. Such a torque you would think is trying to line up the magnet with the field, but it only causes the precession. If we want to change the angle of the gyroscope with respect to the $z$-axis, we must exert a torque on it about the $z$-axis. If we apply a torque which goes in the same direction as the precession, the angle of the gyroscope will change to give a smaller component of $\FLPJ$ in the $z$-direction. In Fig. 35-3, the angle between $\FLPJ$ and the $z$-axis would increase. If we try to hinder the precession, $\FLPJ$ moves toward the vertical.
For our precessing atom in a uniform magnetic field, how can we apply the kind of torque we want? The answer is: with a weak magnetic field from the side. You might at first think that the direction of this magnetic field would have to rotate with the precession of the magnetic moment, so that it was always at right angles to the moment, as indicated by the field $B'$ in Fig. 35-4(a). Such a field works very well, but an alternating horizontal field is almost as good. If we have a small horizontal field $B'$, which is always in the $x$-direction (plus or minus) and which oscillates with the frequency $\omega_p$, then on each one-half cycle the torque on the magnetic moment reverses, so that it has a cumulative effect which is almost as effective as a rotating magnetic field. Classically, then, we would expect the component of the magnetic moment along the $z$-direction to change if we have a very weak oscillating magnetic field at a frequency which is exactly $\omega_p$. Classically, of course, $\mu_z$ would change continuously, but in quantum mechanics the $z$-component of the magnetic moment cannot adjust continuously. It must jump suddenly from one value to another. We have made the comparison between the consequences of classical mechanics and quantum mechanics to give you some clue as to what might happen classically and how it is related to what actually happens in quantum mechanics. You will notice, incidentally, that the expected resonant frequency is the same in both cases.
One additional remark: From what we have said about quantum mechanics, there is no apparent reason why there couldn’t also be transitions at the frequency $2\omega_p$. It happens that there isn’t any analog of this in the classical case, and also it doesn’t happen in the quantum theory either—at least not for the particular method of inducing the transitions that we have described. With an oscillating horizontal magnetic field, the probability that a frequency $2\omega_p$ would cause a jump of two steps at once is zero. It is only at the frequency $\omega_p$ that transitions, either upward or downward, are likely to occur.
Now we are ready to describe Rabi’s method for measuring magnetic moments. We will consider here only the operation for atoms with a spin of $1/2$. A diagram of the apparatus is shown in Fig. 35-5. There is an oven which gives out a stream of neutral atoms which passes down a line of three magnets. Magnet $1$ is just like the one in Fig. 35-2, and has a field with a strong field gradient—say, with $\ddpl{B_z}{z}$ positive. If the atoms have a magnetic moment, they will be deflected downward if $J_z=+\hbar/2$, or upward if $J_z=-\hbar/2$ (since for electrons $\FLPmu$ is directed opposite to $\FLPJ$). If we consider only those atoms which can get through the slit $S_1$, there are two possible trajectories, as shown. Atoms with $J_z=+\hbar/2$ must go along curve $a$ to get through the slit, and those with $J_z=-\hbar/2$ must go along curve $b$. Atoms which start out from the oven along other paths will not get through the slit.
Magnet $2$ has a uniform field. There are no forces on the atoms in this region, so they go straight through and enter magnet $3$. Magnet $3$ is just like magnet $1$ but with the field inverted, so that $\ddpl{B_z}{z}$ has the opposite sign. The atoms with $J_z=+\hbar/2$ (we say “with spin up”), that felt a downward push in magnet $1$, get an upward push in magnet $3$; they continue on the path $a$ and go through slit $S_2$ to a detector. The atoms with $J_z=-\hbar/2$ (“with spin down”) also have opposite forces in magnets $1$ and $3$ and go along the path $b$, which also takes them through slit $S_2$ to the detector.
The detector may be made in various ways, depending on the atom being measured. For example, for atoms of an alkali metal like sodium, the detector can be a thin, hot tungsten wire connected to a sensitive current meter. When sodium atoms land on the wire, they are evaporated off as Na$^+$ ions, leaving an electron behind. There is a current from the wire proportional to the number of sodium atoms arriving per second.
In the gap of magnet $2$ there is a set of coils that produces a small horizontal magnetic field $\FLPB'$. The coils are driven with a current which oscillates at a variable frequency $\omega$. So between the poles of magnet $2$ there is a strong, constant, vertical field $\FLPB_0$ and a weak, oscillating, horizontal field $\FLPB'$.
Suppose now that the frequency $\omega$ of the oscillating field is set at $\omega_p$—the “precession” frequency of the atoms in the field $\FLPB$. The alternating field will cause some of the atoms passing by to make transitions from one $J_z$ to the other. An atom whose spin was initially “up” ($J_z=+\hbar/2$) may be flipped “down” ($J_z=-\hbar/2$). Now this atom has the direction of its magnetic moment reversed, so it will feel a downward force in magnet $3$ and will move along the path $a'$, shown in Fig. 35-5. It will no longer get through the slit $S_2$ to the detector. Similarly, some of the atoms whose spins were initially down ($J_z=-\hbar/2$) will have their spins flipped up ($J_z=+\hbar/2$) as they pass through magnet $2$. They will then go along the path $b'$ and will not get to the detector.
If the oscillating field $\FLPB'$ has a frequency appreciably different from $\omega_p$, it will not cause any spin flips, and the atoms will follow their undisturbed paths to the detector. So you can see that the “precession” frequency $\omega_p$ of the atoms in the field $\FLPB_0$ can be found by varying the frequency $\omega$ of the field $\FLPB'$ until a decrease is observed in the current of atoms arriving at the detector. A decrease in the current will occur when $\omega$ is “in resonance” with $\omega_p$. A plot of the detector current as a function of $\omega$ might look like the one shown in Fig. 35-6. Knowing $\omega_p$, we can obtain the $g$-value of the atom.
Such atomic-beam or, as they are usually called, “molecular” beam resonance experiments are a beautiful and delicate way of measuring the magnetic properties of atomic objects. The resonance frequency $\omega_p$ can be determined with great precision—in fact, with a greater precision than we can measure the magnetic field $\FLPB_0$, which we must know to find $g$.
35–4The paramagnetism of bulk materials
We would like now to describe the phenomenon of the paramagnetism of bulk materials. Suppose we have a substance whose atoms have permanent magnetic moments, for example a crystal like copper sulfate. In the crystal there are copper ions whose inner electron shells have a net angular momentum and a net magnetic moment. So the copper ion is an object which has a permanent magnetic moment. Let’s say just a word about which atoms have magnetic moments and which ones don’t. Any atom, like sodium for instance, which has an odd number of electrons, will have a magnetic moment. Sodium has one electron in its unfilled shell. This electron gives the atom a spin and a magnetic moment. Ordinarily, however, when compounds are formed the extra electrons in the outside shell are coupled together with other electrons whose spin directions are exactly opposite, so that all the angular momenta and magnetic moments of the valence electrons usually cancel out. That’s why, in general, molecules do not have a magnetic moment. Of course if you have a gas of sodium atoms, there is no such cancellation.1 Also, if you have what is called in chemistry a “free radical”—an object with an odd number of valence electrons—then the bonds are not completely satisfied, and there is a net angular momentum.
In most bulk materials there is a net magnetic moment only if there are atoms present whose inner electron shell is not filled. Then there can be a net angular momentum and a magnetic moment. Such atoms are found in the “transition element” part of the periodic table—for instance, chromium, manganese, iron, nickel, cobalt, palladium, and platinum are elements of this kind. Also, all of the rare earth elements have unfilled inner shells and permanent magnetic moments. There are a couple of other strange things that also happen to have magnetic moments, such as liquid oxygen, but we will leave it to the chemistry department to explain the reason.
Now suppose that we have a box full of atoms or molecules with permanent moments—say a gas, or a liquid, or a crystal. We would like to know what happens if we apply an external magnetic field. With no magnetic field, the atoms are kicked around by the thermal motions, and the moments wind up pointing in all directions. But when there is a magnetic field, it acts to line up the little magnets; then there are more moments lying toward the field than away from it. The material is “magnetized.”
We define the magnetization $\FLPM$ of a material as the net magnetic moment per unit volume, by which we mean the vector sum of all the atomic magnetic moments in a unit volume. If there are $N$ atoms per unit volume and their average moment is $\av{\FLPmu}$ then $\FLPM$ can be written as $N$ times the average atomic moment: \begin{equation} \label{Eq:II:35:8} \FLPM=N\av{\FLPmu}. \end{equation} The definition of $\FLPM$ corresponds to the definition of the electric polarization $\FLPP$ of Chapter 10.
The classical theory of paramagnetism is just like the theory of the dielectric constant we showed you in Chapter 11. One assumes that each of the atoms has a magnetic moment $\FLPmu$, which always has the same magnitude but which can point in any direction. In a field $\FLPB$, the magnetic energy is $-\FLPmu\cdot\FLPB=-\mu B\cos\theta$, where $\theta$ is the angle between the moment and the field. From statistical mechanics, the relative probability of having any angle is $e^{-\text{energy}/kT}$, so angles near zero are more likely than angles near $\pi$. Proceeding exactly as we did in Section 11-3, we find that for small magnetic fields $\FLPM$ is directed parallel to $\FLPB$ and has the magnitude \begin{equation} \label{Eq:II:35:9} M=\frac{N\mu^2B}{3kT}. \end{equation} [See Eq. (11.20).] This approximate formula is correct only for $\mu B/kT$ much less than one.
We find that the induced magnetization—the magnetic moment per unit volume—is proportional to the magnetic field. This is the phenomenon of paramagnetism. You will see that the effect is stronger at lower temperatures and weaker at higher temperatures. When we put a field on a substance, it develops, for small fields, a magnetic moment proportional to the field. The ratio of $M$ to $B$ (for small fields) is called the magnetic susceptibility.
Now we want to look at paramagnetism from the point of view of quantum mechanics. We take first the case of an atom with a spin of $1/2$. In the absence of a magnetic field the atoms have a certain energy, but in a magnetic field there are two possible energies, one for each value of $J_z$. For $J_z=+\hbar/2$, the energy is changed by the magnetic field by the amount \begin{equation} \label{Eq:II:35:10} \Delta U_1=+g\biggl(\frac{q_e\hbar}{2m}\biggr)\cdot\frac{1}{2}\cdot B. \end{equation} (The energy shift $\Delta U$ is positive for an atom because the electron charge is negative.) For $J_z=-\hbar/2$, the energy is changed by the amount \begin{equation} \label{Eq:II:35:11} \Delta U_2=-g\biggl(\frac{q_e\hbar}{2m}\biggr)\cdot\frac{1}{2}\cdot B. \end{equation} To save writing, let’s set \begin{equation} \label{Eq:II:35:12} \mu_0=g\biggl(\frac{q_e\hbar}{2m}\biggr)\cdot\frac{1}{2}; \end{equation} then \begin{equation} \label{Eq:II:35:13} \Delta U=\pm\mu_0B. \end{equation} The meaning of $\mu_0$ is clear: $-\mu_0$ is the $z$-component of the magnetic moment in the up-spin case, and $+\mu_0$ is the $z$-component of the magnetic moment in the down-spin case.
Now statistical mechanics tells us that the probability that an atom is in one state or another is proportional to \begin{equation*} e^{-(\text{Energy of state})/kT}. \end{equation*} With no magnetic field the two states have the same energy; so when there is equilibrium in a magnetic field, the probabilities are proportional to \begin{equation} \label{Eq:II:35:14} e^{-\Delta U/kT}. \end{equation} The number of atoms per unit volume with spin up is \begin{equation} \label{Eq:II:35:15} N_{\text{up}}=ae^{-\mu_0B/kT}, \end{equation} and the number with spin down is \begin{equation} \label{Eq:II:35:16} N_{\text{down}}=ae^{+\mu_0B/kT}. \end{equation} The constant $a$ is to be determined so that \begin{equation} \label{Eq:II:35:17} N_{\text{up}}+N_{\text{down}}=N, \end{equation} the total number of atoms per unit volume. So we get that \begin{equation} \label{Eq:II:35:18} a=\frac{N}{e^{+\mu_0B/kT}+e^{-\mu_0B/kT}}. \end{equation}
What we are interested in is the average magnetic moment along the $z$-axis. The atoms with spin up will contribute a moment of $-\mu_0$, and those with spin down will have a moment of $+\mu_0$; so the average moment is \begin{equation} \label{Eq:II:35:19} \av{\mu} = \frac{N_{\text{up}}(-\mu_0)+N_{\text{down}}(+\mu_0)}{N}. \end{equation}
The magnetic moment per unit volume $M$ is then $N\av{\mu}$. Using Eqs. (35.15), (35.16), and (35.17), we get that \begin{equation} \label{Eq:II:35:20} M=N\mu_0\, \frac{e^{+\mu_0B/kT}-e^{-\mu_0B/kT}}{e^{+\mu_0B/kT}+e^{-\mu_0B/kT}}. \end{equation} This is the quantum-mechanical formula for $M$ for atoms with $j=1/2$. Incidentally, this formula can also be written somewhat more concisely in terms of the hyperbolic tangent function: \begin{equation} \label{Eq:II:35:21} M=N\mu_0\,\tanh\frac{\mu_0B}{kT}. \end{equation}
A plot of $M$ as a function of $B$ is given in Fig. 35-7. When $B$ gets very large, the hyperbolic tangent approaches $1$, and $M$ approaches the limiting value $N\mu_0$. So at high fields, the magnetization saturates. We can see why that is; at high enough fields the moments are all lined up in the same direction. In other words, they are all in the spin-down state, and each atom contributes the moment $\mu_0$.
In most normal cases—say, for typical moments, room temperatures, and the fields one can normally get (like $10{,}000$ gauss)—the ratio $\mu_0B/kT$ is about $0.002$. One must go to very low temperatures to see the saturation. For normal temperatures, we can usually replace $\tanh x$ by $x$, and write \begin{equation} \label{Eq:II:35:22} M=\frac{N\mu_0^2B}{kT}. \end{equation}
Just as we saw in the classical theory, $M$ is proportional to $B$. In fact, the formula is almost exactly the same, except that there seems to be a factor of $1/3$ missing. But we still need to relate the $\mu_0$ in our quantum formula to the $\mu$ that appears in the classical result, Eq. (35.9).
In the classical formula, what appears is $\mu^2=\FLPmu\cdot\FLPmu$, the square of the vector magnetic moment, or \begin{equation} \label{Eq:II:35:23} \FLPmu\cdot\FLPmu=\biggl(g\,\frac{q_e}{2m}\biggr)^2\FLPJ\cdot\FLPJ. \end{equation} We pointed out in the last chapter that you can very likely get the right answer from a classical calculation by replacing $\FLPJ\cdot\FLPJ$ by $j(j+1)\hbar^2$. In our particular example, we have $j=1/2$, so \begin{equation*} j(j+1)\hbar^2=\tfrac{3}{4}\hbar^2. \end{equation*} Substituting this for $\FLPJ\cdot\FLPJ$ in Eq. (35.23), we get \begin{equation*} \FLPmu\cdot\FLPmu=\biggl(g\,\frac{q_e}{2m}\biggr)^2 \frac{3\hbar^2}{4}, \end{equation*} or in terms of $\mu_0$, defined in Eq. (35.12), we get \begin{equation*} \FLPmu\cdot\FLPmu=3\mu_0^2. \end{equation*} Substituting this for $\mu^2$ in the classical formula, Eq. (35.9), does indeed reproduce the correct quantum formula, Eq. (35.22).
The quantum theory of paramagnetism is easily extended to atoms of any spin $j$. The low-field magnetization is \begin{equation} \label{Eq:II:35:24} M=Ng^2\,\frac{j(j+1)}{3}\,\frac{\mu_B^2B}{kT}, \end{equation} where \begin{equation} \label{Eq:II:35:25} \mu_B=\frac{q_e\hbar}{2m} \end{equation} is a combination of constants with the dimensions of a magnetic moment. Most atoms have moments of roughly this size. It is called the Bohr magneton. The spin magnetic moment of the electron is almost exactly one Bohr magneton.
2020.9.7: 추정 및 계산
$\tanh x$를 $x$로 대체한다? 이게 뭔 소리? 하고 그림 35-7를 보다. 간단한 계산으로 x는 원점에서의 $\tanh x$의 접선이 입증되기에, 0에 가까운 값은 접선 $x$로 근사시킨다고 추정.
입증을 위한 계산 돌입.
먼저
$ \text{평균 moment}= \frac{\sum_{i=0}^{2j}e^{\frac{\mu_iB}{kT}}\mu_i}{\sum_{i=0}^{2j}e^{\frac{\mu_iB}{kT}}},\, 여기서 \,\mu_i=g\biggl(\frac{q_e\hbar}{2m}\biggr)(-j+i);\\
\mu_B=\frac{q_e\hbar}{2m}\,, x=\frac{g\mu_BB}{kT} \text{라고 놓으면}\\
\frac{\mu_iB}{kT}=gB\frac{q_e\hbar}{2mkT}(-j+i)=\frac{gB\mu_B}{kT}(-j+i)=x(-j+i)
\\
\text{평균 moment}=\frac{\sum_{i=0}^{2j}e^{x(-j+i)}g\mu_B(-j+i)}{\sum_{i=0}^{2j}e^{x(-j+i)}}
=\frac{g\mu_B\sum_{i=0}^{2j}e^{x(-j+i)}(-j+i)}{\sum_{i=0}^{2j}e^{x(-j+i)}}
={g\mu_B}\frac{{\sum_{i=0}^{2j}(i+1)e^{ix}}-(j+1){\sum_{i=0}^{2j}e^{ix}}}{\sum_{i=0}^{2j}e^{ix}}
\\ \sum_{i=0}^{2j}(i+1)e^{ix}=\frac{d(\sum_{i=0}^{2j}e^{(i+1)x})}{de^x}=
\frac{d(\frac{e^x-e^{(2j+2)x}}{1-e^x})}{de^x}=\frac{1-(2j+2)e^{(2j+1)x}+(2j+1)e^{(2j+2)x}}{(1-e^x)^2}\,와\, \sum_{i=0}^{2j}e^{ix}=\frac{1-e^{(2j+1)x}}{1-e^x}
\\ \text{를 대입하면} $
$\text{average moment}=
g\mu_B\frac{{1-(2j+2)e^{(2j+1)x}+(2j+1)e^{(2j+2)x}}-(j+1)(1-e^x)(1-e^{(2j+1)x})}{(1-e^x)(1-e^{(2j+1)x})}
\\=g\mu_B\frac{-j+(j+1)e^x+je^{(2j+2)x}-(j+1)e^{(2j+1)x}}{(1-e^x)(1-e^{(2j+1)x})}
\\ \text{정신 사나운 복잡함을 덜기 위해 } m=2j+2, n=2j+1 \text{ 라고 하자}
\\
=g\mu_B\frac{-j+(j+1)e^x+je^{mx}-(j+1)e^{nx}}{(1-e^x)(1-e^{nx})}=F(x),
F'(0) \text{을 구하기 위하여} F'(x)\text{을 계산해 보면}
\\=\frac{g\mu_B}{(1-e^x)^2(1-e^{nx})^2}\times
\{(jme^{mx}+(j+1)e^x-(j+1)ne^{nx})(1-e^x)(1-e^{nx})-
(-j+(j+1)e^x+je^{mx}-(j+1)e^{nx})(me^{mx}-ne^{nx}-e^x) \}\cdot\cdot\cdot(*)
\\ \text{x=0 => 분모=분자=0. 하여 로피탈(L'Hospital) 정리를 적용하기 전에, 계산을 단순화를 위해 (*)을 둘로 나누자, 즉,}
\\ f(x)(1-e^x)(1-e^{nx}),\, where\, f(x)= (jme^{mx}+(j+1)e^x-(j+1)ne^{nx})
\\u(x)v(x),\, where\,u(x)=-(-j+(j+1)e^x+je^{mx}-(j+1)e^{nx}), v(x)= me^{mx}-ne^{nx}-e^x.
\,g\mu_B \text{는 당분간 생략하고}
\\
\lim_{x\to 0}\frac{f(x)(1-e^x)(1-e^{nx})}{(1-e^x)^2(1-e^{nx})^2}=\lim_{x\to 0}\frac{jme^{mx}+(j+1)e^x-(j+1)ne^{nx}}{(1-e^x)(1-e^{nx})}
\\ \text{여기서 주목할 것은} f(0)=f'(0)=0, \text{그래서}
\\
\lim_{x\to 0}\frac{f(x)}{(1-e^x)(1-e^{nx})}=\lim_{x\to 0}\frac{f''(x)}{((1-e^x)(1-e^{nx}))''}=
=\frac{jm^3+j+1-(j+1)n^3}{2n}=\frac{2nj(j+1)}{2n}=j(j+1)
\\ \text{2번째항, } uv \text{의 경우,}
\\
((1-e^x)^2(1-e^{nx})^2)''''(0)=_4C_2((1-e^x)^2)''(0)((1-e^{nx})^2)''(0)=24n^2,
\\u(0)=u'(0)=u''(0)=v(0)=0,\,u'''(0)=-2j(j+1)n,\, v'(0)=2n
\\
\lim_{x\to 0}\frac{u(x)v(x)}{((1-e^x)(1-e^{nx}))^2}
=\lim_{x\to 0}\frac{(u(x)v(x))''''}{((1-e^x)^2(1-e^{nx})^2)''''}
=\frac{_4C_3u'''(0)v'(0)}{24n^2}=-\frac23j(j+1)
\\F'(0)=g\mu_B\frac{j(j+1)}3, \text{접선은 } F'(0)x=g^2\frac{j(j+1)}3\frac{{\mu_B}^2B}{kT}$
2020.9.11: 이 섹션의 논리를 따르자면, Diamagnetism 들어설 자리가 없어 보인다, 34장에서 반작용 원리로 설명했지만 일관성이 부족하다
35–5Cooling by adiabatic demagnetization
There is a very interesting special application of paramagnetism. At very low temperatures it is possible to line up the atomic magnets in a strong field. It is then possible to get down to extremely low temperatures by a process called adiabatic demagnetization. We can take a paramagnetic salt (for example, one containing a number of rare-earth atoms like praseodymium-ammonium-nitrate), and start by cooling it down with liquid helium to one or two degrees absolute in a strong magnetic field((기를 가둬 두고 헬륨으로 온도 낮추다). Then the factor $\mu B/kT$ is larger than $1$—say more like $2$ or $3$. Most of the spins are lined up, and the magnetization is nearly saturated. Let’s say, to make it easy, that the field is very powerful and the temperature is very low, so that nearly all the atoms are lined up(구조 형성). Then you isolate the salt thermally (say, by removing the liquid helium and leaving a good vacuum) and turn off the magnetic field. The temperature of the salt goes way down.
Now if you were to turn off the field suddenly, the jiggling and shaking of the atoms in the crystal lattice would gradually knock all the spins out of alignment. Some of them would be up and some down. But if there is no field (and disregarding the interactions between the atomic magnets, which will make only a slight error), it takes no energy to turn over the atomic magnets. They could randomize their spins without any energy change and, therefore, without any temperature change.
Suppose, however, that while the atomic magnets are being flipped over by the thermal motion there is still some magnetic field present. Then it requires some work to flip them over opposite to the field—they must do work against the field. This takes energy from the thermal motions and lowers the temperature. So if the strong magnetic field is not removed too rapidly, the temperature of the salt will decrease—it is cooled by the demagnetization. From the quantum-mechanical view, when the field is strong all the atoms are in the lowest state, because the odds against any being in the upper state are impossibly big. But as the field is lowered, it gets more and more likely that thermal fluctuations will knock an atom into the upper state. When that happens, the atom absorbs the energy $\Delta U=\mu_0B$. So if the field is turned off slowly, the magnetic transitions can take energy out of the thermal vibrations of the crystal, cooling it off. It is possible in this way to go from a temperature of a few degrees absolute down to a temperature of a few thousandths of a degree.
Would you like to make something even colder than that? It turns out that Nature has provided a way. We have already mentioned that there are also magnetic moments for the atomic nuclei. Our formulas for paramagnetism work just as well for nuclei, except that the moments of nuclei are roughly a thousand times smaller. [They are of the order of magnitude of $q\hbar/2m_p$, where $m_p$ is the proton mass, so they are smaller by the ratio of the masses of the electron and proton.] With such magnetic moments, even at a temperature of $2^\circ$K, the factor $\mu B/kT$ is only a few parts in a thousand. But if we use the paramagnetic demagnetization process to get down to a temperature of a few thousandths of a degree, $\mu B/kT$ becomes a number near $1$—at these low temperatures we can begin to saturate the nuclear moments. That is good luck, because we can then use the adiabatic demagnetization of the nuclear magnetism to reach still lower temperatures. Thus it is possible to do two stages of magnetic cooling. First we use adiabatic demagnetization of paramagnetic ions to reach a few thousandths of a degree. Then we use the cold paramagnetic salt to cool some material which has a strong nuclear magnetism. Finally, when we remove the magnetic field from this material, its temperature will go down to within a millionth of a degree of absolute zero—if we have done everything very carefully.
35–6Nuclear magnetic resonance
We have said that atomic paramagnetism is very small and that nuclear magnetism is even a thousand times smaller. Yet it is relatively easy to observe the nuclear magnetism by the phenomenon of “nuclear magnetic resonance.” Suppose we take a substance like water, in which all of the electron spins are exactly balanced so that their net magnetic moment is zero. The molecules will still have a very, very tiny magnetic moment due to the nuclear magnetic moment of the hydrogen nuclei. Suppose we put a small sample of water in a magnetic field $\FLPB$. Since the protons (of the hydrogen) have a spin of $1/2$, they will have two possible energy states. If the water is in thermal equilibrium, there will be slightly more protons in the lower energy states—with their moments directed parallel to the field. There is a small net magnetic moment per unit volume. Since the proton moment is only about one-thousandth of an atomic moment, the magnetization which goes as $\mu^2$—using Eq. (35.22)—is only about one-millionth as strong as typical atomic paramagnetism. (That’s why we have to pick a material with no atomic magnetism.) If you work it out, the difference between the number of protons with spin up and with spin down is only one part in $10^8$, so the effect is indeed very small! It can still be observed, however, in the following way.
Suppose we surround the water sample with a small coil that produces a small horizontal oscillating magnetic field. If this field oscillates at the frequency $\omega_p$, it will induce transitions between the two energy states—just as we described for the Rabi experiment in Section 35-3. When a proton flips from an upper energy state to a lower one, it will give up the energy $2\mu_zB$ which, as we have seen, is equal to $\hbar\omega_p$. If it flips from the lower energy state to the upper one, it will absorb the energy $\hbar\omega_p$ from the coil. Since there are slightly more protons in the lower state than in the upper one, there will be a net absorption of energy from the coil. Although the effect is very small, the slight energy absorption can be seen with a sensitive electronic amplifier.
Just as in the Rabi molecular-beam experiment, the energy absorption will be seen only when the oscillating field is in resonance, that is, when \begin{equation*} \omega=\omega_p=g\biggl(\frac{q_e}{2m_p}\biggr)B. \end{equation*} It is often more convenient to search for the resonance by varying $B$ while keeping $\omega$ fixed. The energy absorption will evidently appear when \begin{equation*} B=\frac{2m_p}{gq_e}\,\omega. \end{equation*}
A typical nuclear magnetic resonance apparatus is shown in Fig. 35-8. A high-frequency oscillator drives a small coil placed between the poles of a large electromagnet. Two small auxiliary coils around the pole tips are driven with a $60$-cycle current so that the magnetic field is “wobbled” about its average value by a very small amount. As an example, say that the main current of the magnet is set to give a field of $5000$ gauss, and the auxiliary coils produce a variation of $\pm1$ gauss about this value. If the oscillator is set at $21.2$ megacycles per second, it will then be at the proton resonance each time the field sweeps through $5000$ gauss [using Eq. (34.13) with $g=5.58$ for the proton].
2020.9.11: 그림 35-8 정리
1. 큰 전자 자석은 물의 양성자들 세차 운동을 만들고 그 운동의 '특정 주기'는 보조에 의해 작은 변화를 갖는다, 그 이유는 양성자 세차 주기가 약간씩 다르기 때문이란다(?).
2. oscillator는 위 1의 특정 주기로 진동함으로써, 양성자의 낮은 에너지 상태에서 높은 상태로의 변환을 위한 에너지를 공급한다.(* Rabi의 방법...so that it has a 'cumulative effect' which is almost as effective as a rotating magnetic field, 파인만 강의 II, 35-5)
그러한 에너지 변환이 생기는 순간, oscillator는 파워를 상실할 것이고 그 상실 신호는 아래 오실로스코프에서 높낮이로 나타나도록 되어있다.
*여기서 의문은 oscillator의 주기만 언급되고 그 진동의 크기에 대하여는 언급이 없다. 아무리 작은 크기라도 관계없다는 건가? cumulative라는 표현으로 보아 작더라도 축적되어 효과를 본다는 말인가? 파도 속의 돛배... 해류와 같은 전자파 흐름 속에서 세차운동하는 양성자를 파도가 지속적으로 흔들어 그 흐름을 뚫고 나오게 하는 것이지 싶다. 지구의 밀물 설물, 대기의 움직임도 지구의 자기로 설명할 수 있을 거다
2023.2.7: cumulative와 같은 의미로 사용된 piling up
The circuit of the oscillator is arranged to give an additional output signal proportional to any change in the power being absorbed from the oscillator. This signal is fed to the vertical deflection amplifier of an oscilloscope. The horizontal sweep of the oscilloscope is triggered once during each cycle of the field-wobbling frequency. (More usually, the horizontal deflection is made to follow in proportion to the wobbling field.)
Before the water sample is placed inside the high-frequency coil, the power drawn from the oscillator is some value. (It doesn’t change with the magnetic field.) When a small bottle of water is placed in the coil, however, a signal appears on the oscilloscope, as shown in the figure. We see a picture of the power being absorbed by the flipping over of the protons!
In practice, it is difficult to know how to set the main magnet to exactly $5000$ gauss. What one does is to adjust the main magnet current until the resonance signal appears on the oscilloscope. It turns out that this is now the most convenient way to make an accurate measurement of the strength of a magnetic field. Of course, at some time someone had to measure accurately the magnetic field and frequency to determine the $g$-value of the proton. But now that this has been done, a proton resonance apparatus like that of the figure can be used as a “proton resonance magnetometer.”
We should say a word about the shape of the signal. If we were to wobble the magnetic field very slowly, we would expect to see a normal resonance curve. The energy absorption would read a maximum when $\omega_p$ arrived exactly at the oscillator frequency. There would be some absorption at nearby frequencies because all the protons are not in exactly the same field—and different fields mean slightly different resonant frequencies.
One might wonder, incidentally, whether at the resonance frequency we should see any signal at all. Shouldn’t we expect the high-frequency field to equalize the populations of the two states—so that there should be no signal except when the water is first put in? Not exactly, because although we are trying to equalize the two populations, the thermal motions on their part are trying to keep the proper ratios for the temperature $T$. If we sit at the resonance, the power being absorbed by the nuclei is just what is being lost to the thermal motions. There is, however, relatively little “thermal contact” between the proton magnetic moments and the atomic motions. The protons are relatively isolated down in the center of the electron distributions. So in pure water, the resonance signal is, in fact, usually too small to be seen. To increase the absorption, it is necessary to increase the “thermal contact.” This is usually done by adding a little iron oxide to the water. The iron atoms are like small magnets; as they jiggle around in their thermal dance, they make tiny jiggling magnetic fields at the protons. These varying fields “couple” the proton magnets to the atomic vibrations and tend to establish thermal equilibrium. It is through this “coupling” that protons in the higher energy states can lose their energy so that they are again capable of absorbing energy from the oscillator.
21.10.18: Poincare-Hopf 정리에 의해서, 에너지 흡수는 수학적으로 전자기장이 형성하는 2차원 surface를 connected sum하는 것.
In practice the output signal of a nuclear resonance apparatus does not look like a normal resonance curve. It is usually a more complicated signal with oscillations—like the one drawn in the figure. Such signal shapes appear because of the changing fields. The explanation should be given in terms of quantum mechanics, but it can be shown that in such experiments the classical ideas of precessing moments always give the correct answer. Classically, we would say that when we arrive at resonance we start driving a lot of the precessing nuclear magnets synchronously. In so doing, we make them precess together. These nuclear magnets, all rotating together, will set up an induced emf in the oscillator coil at the frequency $\omega_p$. But because the magnetic field is increasing with time, the precession frequency is increasing also, and the induced voltage is soon at a frequency a little higher than the oscillator frequency. As the induced emf goes alternately in phase and out of phase with the oscillator, the “absorbed” power goes alternately positive and negative. So on the oscilloscope we see the beat note between the proton frequency and the oscillator frequency. Because the proton frequencies are not all identical (different protons are in slightly different fields) and also possibly because of the disturbance from the iron oxide in the water, the freely precessing moments soon get out of phase, and the beat signal disappears.
These phenomena of magnetic resonance have been put to use in many ways as tools for finding out new things about matter—especially in chemistry and nuclear physics. It goes without saying that the numerical values of the magnetic moments of nuclei tell us something about their structure. In chemistry, much has been learned from the structure (or shape) of the resonances. Because of magnetic fields produced by nearby nuclei, the exact position of a nuclear resonance is shifted somewhat, depending on the environment in which any particular nucleus finds itself. Measuring these shifts helps determine which atoms are near which other ones and helps to elucidate the details of the structure of molecules. Equally important is the electron spin resonance of free radicals. Although not present to any very large extent in equilibrium, such radicals are often intermediate states of chemical reactions. A measurement of an electron spin resonance is a delicate test for the presence of free radicals and is often the key to understanding the mechanism of certain chemical reactions.
- Ordinary Na vapor is mostly monatomic, although there are also some molecules of $\text{Na}_2$. ↩