Some time ago we discussed in considerable detail the properties of light waves and their interference—that is, the effects of the superposition of two waves from different sources. In all these analyses we assumed that the frequencies of the sources were all the same. In this chapter we shall discuss some of the phenomena which result from the interference of two sources which have different frequencies.

It is easy to guess what is going to happen. Proceeding in the same way as we have done previously, suppose we have two equal oscillating sources of the same frequency whose phases are so adjusted, say, that the signals arrive in phase at some point $P$. At that point, if it is light, the light is very strong; if it is sound, it is very loud; or if it is electrons, many of them arrive. On the other hand, if the arriving signals were $180^\circ$ out of phase, we would get no signal at $P$, because the net amplitude there is then a minimum. Now suppose that someone twists the “phase knob” of one of the sources and changes the phase at $P$ back and forth, say, first making it $0^\circ$ and then $180^\circ$, and so on. Of course, we would then find variations in the net signal strength. Now we also see that if the phase of one source is slowly changing relative to that of the other in a gradual, uniform manner, starting at zero, going up to ten, twenty, thirty, forty degrees, and so on, then what we would measure at $P$ would be a series of strong and weak “pulsations,” because when the phase shifts through $360^\circ$ the amplitude returns to a maximum. Of course, to say that one source is shifting its phase relative to another at a uniform rate is the same as saying that the number of oscillations per second is slightly different for the two.

So we know the answer: if we have two sources at slightly different frequencies we should find, as a net result, an oscillation with a slowly pulsating intensity. That is all there really is to the subject!

It is very easy to formulate this result mathematically also. Suppose, for example, that we have two waves, and that we do not worry for the moment about all the spatial relations, but simply analyze what arrives at $P$. From one source, let us say, we would have $\cos\omega_1t$, and from the other source, $\cos\omega_2t$, where the two $\omega$’s are not exactly the same. Of course the amplitudes may not be the same, either, but we can solve the general problem later; let us first take the case where the amplitudes are equal. Then the total amplitude at $P$ is the sum of these two cosines. If we plot the amplitudes of the waves against the time, as in Fig. 48–1, we see that where the crests coincide we get a strong wave, and where a trough and crest coincide we get practically zero, and then when the crests coincide again we get a strong wave again.

Mathematically, we need only to add two cosines and rearrange the result somehow. There exist a number of useful relations among cosines which are not difficult to derive. Of course we know that \begin{equation} \label{Eq:I:48:1} e^{i(a + b)} = e^{ia}e^{ib}, \end{equation} and that $e^{ia}$ has a real part, $\cos a$, and an imaginary part, $\sin a$. If we take the real part of $e^{i(a + b)}$, we get $\cos\,(a + b)$. If we multiply out: \begin{equation*} e^{ia}e^{ib} = (\cos a + i\sin a)(\cos b + i\sin b), \end{equation*} we get $\cos a\cos b - \sin a\sin b$, plus some imaginary parts. But we now need only the real part, so we have \begin{equation} \label{Eq:I:48:2} \cos\,(a + b) = \cos a\cos b - \sin a\sin b. \end{equation} Now if we change the sign of $b$, since the cosine does not change sign while the sine does, the same equation, for negative $b$, is \begin{equation} \label{Eq:I:48:3} \cos\,(a - b) = \cos a\cos b + \sin a\sin b. \end{equation} If we add these two equations together, we lose the sines and we learn that the product of two cosines is half the cosine of the sum, plus half the cosine of the difference: \begin{equation} \label{Eq:I:48:4} \cos a\cos b = \tfrac{1}{2}\cos\,(a + b) + \tfrac{1}{2}\cos\,(a - b). \end{equation} Now we can also reverse the formula and find a formula for $\cos\alpha + \cos\beta$ if we simply let $\alpha = a + b$ and $\beta = a - b$. That is, $a = \tfrac{1}{2}(\alpha + \beta)$ and $b = \tfrac{1}{2}(\alpha - \beta)$, so that \begin{equation} \label{Eq:I:48:5} \cos\alpha + \cos\beta = 2\cos\tfrac{1}{2}(\alpha + \beta) \cos\tfrac{1}{2}(\alpha - \beta). \end{equation}

Now we can analyze our problem. The sum of $\cos\omega_1t$ and $\cos\omega_2t$ is \begin{equation} \label{Eq:I:48:6} \cos\omega_1t + \cos\omega_2t = 2\cos\tfrac{1}{2}(\omega_1 + \omega_2)t \cos\tfrac{1}{2}(\omega_1 - \omega_2)t. \end{equation} Now let us suppose that the two frequencies are nearly the same, so that $\tfrac{1}{2}(\omega_1 + \omega_2)$ is the average frequency, and is more or less the same as either(* 양 주파수와 똑같은 크기로 작고 크다). But $\omega_1 - \omega_2$ is much smaller than $\omega_1$ or $\omega_2$ because, as we suppose, $\omega_1$ and $\omega_2$ are nearly equal. That means that we can represent the solution by saying that there is a high-frequency cosine wave more or less like the ones we started with, but that its “size” is slowly changing—its “size” is pulsating with a frequency which appears to be $\tfrac{1}{2}(\omega_1 - \omega_2)$. But is this the frequency at which the beats are heard? Although (48.6) says that the amplitude goes as $\cos\tfrac{1}{2}(\omega_1 - \omega_2)t$, what it is really telling us is that the high-frequency oscillations are contained between two opposed cosine curves (shown dotted in Fig. 48–1). On this basis one could say that the amplitude varies at the frequency $\tfrac{1}{2}(\omega_1 - \omega_2)$, but if we are talking about the intensity of the wave we must think of it as having twice this frequency. That is, the modulation of the amplitude, in the sense of the strength of its intensity, is at frequency $\omega_1 - \omega_2$, although the formula tells us that we multiply by a cosine wave at half that frequency. The technical basis for the difference is that the high frequency-wave has a little different phase relationship in the second half-cycle.

Ignoring this small complication, we may conclude that if we add two waves of frequency $\omega_1$ and $\omega_2$, we will get a net resulting wave of average frequency $\tfrac{1}{2}(\omega_1 + \omega_2)$ which oscillates in strength with a frequency $\omega_1 - \omega_2$.

If the two amplitudes are different, we can do it all over again by multiplying the cosines by different amplitudes $A_1$ and $A_2$, and do a lot of mathematics, rearranging, and so on, using equations like (48.2)–(48.5). However, there are other, easier ways of doing the same analysis. For example, we know that it is much easier to work with exponentials than with sines and cosines and that we can represent $A_1\cos\omega_1t$ as the real part of $A_1e^{i\omega_1t}$. The other wave would similarly be the real part of $A_2e^{i\omega_2t}$. If we add the two, we get $A_1e^{i\omega_1t} + A_2e^{i\omega_2t}$. If we then factor out the average frequency, we have \begin{equation} \label{Eq:I:48:7} A_1e^{i\omega_1t} + A_2e^{i\omega_2t} = e^{i(\omega_1 + \omega _2)t/2}[ A_1e^{i(\omega_1 - \omega _2)t/2} + A_2e^{-i(\omega_1 - \omega_2)t/2}]. \end{equation} Again we have the high-frequency wave with a modulation at the lower frequency.

If we are now asked for the intensity of the wave of Eq. (48.7), we can either take the absolute square of the left side, or of the right side. Let us take the left side. The intensity then is \begin{equation} \label{Eq:I:48:8} I = A_1^2 + A_2^2 + 2A_1A_2\cos\,(\omega_1 - \omega_2)t. \end{equation} We see that the intensity swells and falls at a frequency $\omega_1 - \omega_2$, varying between the limits $(A_1 + A_2)^2$ and $(A_1 - A_2)^2$. If $A_1 \neq A_2$, the minimum intensity is not zero.

One more way to represent this idea is by means of a drawing, like Fig. 48–2. We draw a vector of length $A_1$, rotating at a frequency $\omega_1$, to represent one of the waves in the complex plane. We draw another vector of length $A_2$, going around at a frequency $\omega_2$, to represent the second wave. If the two frequencies are exactly equal, their resultant is of fixed length as it keeps revolving, and we get a definite, fixed intensity from the two. But if the frequencies are slightly different, the two complex vectors go around at different speeds. Figure 48–3 shows what the situation looks like relative to the vector $A_1e^{i\omega_1t}$. We see that $A_2$ is turning slowly away from $A_1$, and so the amplitude that we get by adding the two is first strong, and then, as it opens out, when it gets to the $180^\circ$ relative position the resultant gets particularly weak, and so on. As the vectors go around, the amplitude of the sum vector gets bigger and smaller, and the intensity thus pulsates. It is a relatively simple idea, and there are many different ways of representing the same thing.

The effect is very easy to observe experimentally. In the case of acoustics, we may arrange two loudspeakers driven by two separate oscillators, one for each loudspeaker, so that they each make a tone. We thus receive one note from one source and a different note from the other source. If we make the frequencies exactly the same, the resulting effect will have a definite strength at a given space location. If we then de-tune them a little bit, we hear some variations in the intensity. The farther they are de-tuned, the more rapid are the variations of sound. The ear has some trouble following variations more rapid than ten or so per second.

We may also see the effect on an oscilloscope which simply displays the sum of the currents to the two speakers. If the frequency of pulsing is relatively low, we simply see a sinusoidal wave train whose amplitude pulsates, but as we make the pulsations more rapid we see the kind of wave shown in Fig. 48–1. As we go to greater frequency differences, the “bumps” move closer together. Also, if the amplitudes are not equal and we make one signal stronger than the other, then we get a wave whose amplitude does not ever become zero, just as we expect. Everything works the way it should, both acoustically and electrically.

The opposite phenomenon occurs too!(* 공학적으로 가능!) In radio transmission using so-called amplitude modulation (am), the sound is broadcast by the radio station as follows: the radio transmitter has an ac electric oscillation which is at a very high frequency, for example $800$ kilocycles per second, in the broadcast band. If this carrier signal is turned on, the radio station emits a wave which is of uniform amplitude at $800{,}000$ oscillations a second. The way the “information” is transmitted, the useless kind of information about what kind of car to buy, is that when somebody talks into a microphone the amplitude of the carrier signal is changed in step with the vibrations of sound entering the microphone.(* 착각 주의: 운반 wave와 소리 에너지 wave의 합이 아니라, 진폭이 소리 에너지에 비례하여 변화한다는 얘기)

If we take as the simplest mathematical case the situation where a soprano is singing a perfect note, with perfect sinusoidal oscillations of her vocal cords, then we get a signal whose strength is alternating as shown in Fig. 48–4. The audiofrequency alternation is then recovered in the receiver; we get rid of the carrier wave and just look at the envelope which represents the oscillations of the vocal cords, or the sound of the singer. The loudspeaker then makes corresponding vibrations at the same frequency in the air, and the listener is then essentially unable to tell the difference, so they say. Because of a number of distortions and other subtle effects, it is, in fact, possible to tell whether we are listening to a radio or to a real soprano; otherwise(* distortion, subtle effect 가 없는 경우) the idea is as indicated above.

2022.4.1: 정리 좀 해보자, 헷갈린다
진동수 다른 2개 $\omega_1, \omega_2$ waves => $\frac12 (\omega_1+\omega_2)$ wave with intensity $(\omega_1-\omega_2)$ 'the amplitude of the carrier signal is changed in step with the vibrations of sound entering the microphone' 여기에서 carrrier 진폭을 변화시키는 건 wave 자체가 아니라 소리 에너지!!! wave 의 2배 진동수 갖는.

Mathematically, the modulated wave described above(* 소리 에너지 강약에 춤추는 mathematically simplest 식, 즉 아래) would be expressed as \begin{equation} \label{Eq:I:48:9} S = (1 + b\cos\omega_mt)\cos\omega_ct, \end{equation} where $\omega_c$ represents the frequency of the carrier and $\omega_m$ is the frequency of the audio tone. Again we use all those theorems about the cosines, or we can use $e^{i\theta}$; it makes no difference—it is easier with $e^{i\theta}$, but it is the same thing. We then get \begin{equation} \label{Eq:I:48:10} S = \cos\omega_ct + \tfrac{1}{2}b\cos\,(\omega_c + \omega_m)t + \tfrac{1}{2}b\cos\,(\omega_c - \omega_m)t. \end{equation} So, from another point of view, we can say that the output wave of the system consists of three waves added in superposition: first, the regular wave at the frequency $\omega_c$, that is, at the carrier frequency, and then two new waves at two new frequencies. One is the carrier frequency plus the modulation frequency, and the other is the carrier frequency minus the modulation frequency. If, therefore, we make some kind of plot of the intensity being generated by the generator as a function of frequency, we would find a lot of intensity at the frequency of the carrier, naturally, but when a singer started to sing, we would suddenly also find intensity proportional to the strength of the singer, $b^2$, at frequency $\omega_c + \omega_m$ and $\omega_c - \omega_m$, as shown in Fig. 48–5.

22.4.3: 헷갈림 주의
위 modulated wave 식에 제곱 효과가 포함됨. 다시 말해서, singer intensity는 $b$고 $\omega_c + \omega_m$, $\omega_c - \omega_m$ intensity는 $b^2$.
여기서 중요한 건, modulated wave의 수학적으로 decompose된 3 wave가 따로 구별될 수 있다는 것.
4.6: 설명, 'when somebody talks into a microphone the amplitude of the carrier signal is changed in step with the vibrations of sound entering the microphone'과 (48.9)식의 도출
① 앞 섹션을 고려하면, 소리 에너지로 인한 signal(오디오)과 carrier가 add 되어야 하는 것 같은데... 그러면 $\cos{\omega_c}+\text{const}\times\cos^2{\omega_m}$! (48.9)가 나올 수 가 없다. 헌데
② 설명에만 충실하면, carrier 진폭이 소리 에너지에 맞추어(in step) 변화한다 했으니...
기존 carrier 진폭(* 소리입력이 없을 때, 늘 떠들 수는 없으니) + carrier 진폭 $\times (\text{소리 에너지})$라는 해석도 그럴 듯하고 뒤에 언급되는 side bands는 실험적인 결론일 터 이 해석과 맞아 떨어진다.
그래서 (48.9)가 나온 거라 추정됨.
여기서 주목할 건, 같은 종류 wave가 합칠 때와 달리, acoustical이 마이크를 거쳐 electrical과 합칠 때는 다르다는 거.

2022.6.7: nonlinear response 읽고
여길 와 보니... 시발 뭔 생각하고 썼는지도 모르겠다. 여하튼 4.3일 당시에 뭔가 석연치 않았던 것은 확실하고 그 원인은 nonlinear 효과를 언급/고려하지 않았기 때문으로 이해된다.

These are called side bands; when there is a modulated signal from the transmitter, there are side bands. If there is more than one note at the same time, say $\omega_m$ and $\omega_{m'}$, there are two instruments playing; or if there is any other complicated cosine wave, then, of course, we can see from the mathematics that we get some more waves that correspond to the frequencies $\omega_c \pm \omega_{m'}$.

Therefore, when there is a complicated modulation that can be represented as the sum of many cosines,¹ we find that the actual transmitter is transmitting over a range of frequencies, namely the carrier frequency plus or minus the maximum frequency that the modulation signal contains.

Although at first we might believe that a radio transmitter transmits only at the nominal frequency of the carrier, since there are big, superstable crystal oscillators in there, and everything is adjusted to be at precisely $800$ kilocycles, the moment someone announces that they are at $800$ kilocycles, he modulates the $800$ kilocycles, and so they are no longer precisely at $800$ kilocycles! Suppose that the amplifiers are so built that they are able to transmit over a good range of the ear’s sensitivity (the ear can hear up to $20{,}000$ cycles per second, but usually radio transmitters and receivers do not work beyond $10{,}000$, so we do not hear the highest parts), then, when the man speaks, his voice may contain frequencies ranging up, say, to $10{,}000$ cycles, so the transmitter is transmitting frequencies which may range from $790$ to $810$ kilocycles per second. Now if there were another station at $795$ kc/sec, there would be a lot of confusion. Also, if we made our receiver so sensitive that it picked up only $800$, and did not pick up the $10$ kilocycles on either side, we would not hear what the man was saying, because the information would be on these other frequencies! Therefore it is absolutely essential to keep the stations a certain distance apart, so that their side bands do not overlap and, also, the receiver must not be so selective that it does not permit reception of the side bands as well as of the main nominal frequency.(* 2개 다 못 받는 일이 없도록, 즉 둘 중의 하나는 받아야 한다는 것) In the case of sound, this problem does not really cause much trouble. We can hear over a $\pm20$ kc/sec range, and we have usually from $500$ to $1500$ kc/sec in the broadcast band, so there is plenty of room for lots of stations.

The television problem is more difficult. As the electron beam goes across the face of the picture tube, there are various little spots of light and dark. That “light” and “dark” is the “signal.” Now ordinarily the beam scans over the whole picture, $500$ lines, approximately, in a thirtieth of a second. Let us consider that the resolution of the picture vertically and horizontally is more or less the same, so that there are the same number of spots per inch along a scan line. We want to be able to distinguish dark from light, dark from light, dark from light, over, say, $500$ lines. In order to be able to do this with cosine waves, the shortest wavelength needed thus corresponds to a wavelength, from maximum to maximum, of one $250$th of the screen size. So we have $250\times500\times30$ pieces of information per second. The highest frequency that we are going to carry, therefore, is close to $4$ megacycles per second. Actually, to keep the television stations apart, we have to use a little bit more than this, about $6$ mc/sec; part of it is used to carry the sound signal, and other information. So, television channels are $6$ megacycles per second wide. It certainly would not be possible to transmit tv on an $800$ kc/sec carrier, since we cannot modulate at a higher frequency than the carrier.

4.9: AM은 각 정보를 진폭으로 대응시키는 기계라는 걸 이해했다면, $250\times500\times30=3.75\times 10^6$ 정보들 담으려면 진폭이 최소한 그만큼 필요하다는 거.

At any rate, the television band starts at $54$ megacycles. The first transmission channel, which is channel $2$ (!), has a frequency range from $54$ to $60$ mc/sec, which is $6$ mc/sec wide. “But,” one might say, “we have just proved that there were side bands on both sides, and therefore it should be twice that wide.” It turns out that the radio engineers are rather clever. If we analyze the modulation signal using not just cosine terms, but cosine and sine terms, to allow for phase differences, we then see that there is a definite, invariant relationship between the side band on the high-frequency side and the side band on the low-frequency side. What we mean is that there is no new information on that other side band. So what is done is to suppress one side band, and the receiver is wired inside such that the information which is missing is reconstituted by looking at the single side band and the carrier. Single side-band transmission is a clever scheme for decreasing the band widths needed to transmit information.

The next subject we shall discuss is the interference of waves in both space and time. Suppose that we have two waves travelling in space. We know, of course, that we can represent a wave travelling in space by $e^{i(\omega t - kx)}$. This might be, for example, the displacement in a sound wave. This is a solution of the wave equation provided that $\omega^2 = k^2c^2$, where $c$ is the speed of propagation of the wave. In this case we can write it as $e^{-ik(x - ct)}$, which is of the general form $f(x - ct)$. Therefore this must be a wave which is travelling at this velocity, $\omega/k$, and that is $c$ and everything is all right.

Now we want to add two such waves together. Suppose we have a wave that is travelling with one frequency, and another wave travelling with another frequency. We leave to the reader to consider the case where the amplitudes are different; it makes no real difference. Thus we want to add $e^{i(\omega_1t - k_1x)} + e^{i(\omega_2t - k_2x)}$. We can add these by the same kind of mathematics we used when we added signal waves. Of course, if $c$ is the same for both, this is easy, since it is the same as what we did before: \begin{equation} \label{Eq:I:48:11} e^{i\omega_1(t - x/c)} + e^{i\omega_2(t - x/c)} = e^{i\omega_1t'} + e^{i\omega_2t'}, \end{equation} except that $t' = t - x/c$' is the variable instead of $t$. So we get the same kind of modulations, naturally, but we see, of course, that those modulations are moving along with the wave. In other words, if we added two waves, but these waves were not just oscillating, but also moving in space, then the resultant wave would move along also, at the same speed.

Now we would like to generalize this to the case of waves in which the relationship between the frequency and the wave number $k$ is not so simple. Example: material having an index of refraction. We have already studied the theory of the index of refraction in Chapter 31, where we found that we could write $k = n\omega/c$, where $n$ is the index of refraction. As an interesting example, for x-rays we found that the index $n$ is \begin{equation} \label{Eq:I:48:12} n = 1 - \frac{Nq_e^2}{2\epsO m\omega^2}. \end{equation} We actually derived a more complicated formula in Chapter 31, but this one is as good as any, as an example.

2022.10.1&2: 헛소리, 잘못된 생각으로 헤매다
1. 먼저 $\omega_0=0$으로 놓는 것 => 설명
2. $k =n\omega/c$에서 속도가 느려진다는 걸 phase 속도를 재서 그런건가?
group 속도를 재서 그런 거지. 그렇다면 $\frac{d\omega}{dk}=\frac{c}{n}$인데... 파장에 따라 빛이 분리되는 것과 같은 파장의 그룹속도를 고려하면, $k =n\omega/c$에 문제 없음.
3. 그룹속도를 따지는 걸 보면, 질량은 결국 wave 모임이란 거.
* 다른 생각 => 10.2

Incidentally, we know that even when $\omega$ and $k$ are not linearly proportional, the ratio $\omega/k$ is certainly the speed of propagation for the particular frequency and wave number. We call this ratio the phase velocity; it is the speed at which the phase, or the nodes of a single wave, would move along: \begin{equation} \label{Eq:I:48:13} v_p = \frac{\omega}{k}. \end{equation} This phase velocity, for the case of x-rays in glass, is greater than the speed of light in vacuum (since $n$ in 48.12 is less than $1$), and that is a bit bothersome, because we do not think we can send signals faster than the speed of light!

What we are going to discuss now is the interference of two waves in which $\omega$ and $k$ have a definite formula relating them. The above formula for $n$ says that $k$ is given as a definite function of $\omega$. To be specific, in this particular problem, the formula for $k$ in terms of $\omega$ is \begin{equation} \label{Eq:I:48:14} k = \frac{\omega}{c} - \frac{a}{\omega c}, \end{equation} where $a = Nq_e^2/2\epsO m$, a constant. At any rate, for each frequency there is a definite wave number, and we want to add two such waves together.

Let us do it just as we did in Eq. (48.7): \begin{align} \label{Eq:I:48:15} e^{i(\omega_1t - k_1x)} &+ e^{i(\omega_2t - k_2x)} = e^{i[(\omega_1 + \omega_2)t - (k_1 + k_2)x]/2}\\[1ex] &\times\bigl[ e^{i[(\omega_1 - \omega_2)t - (k_1 - k_2)x]/2} + e^{-i[(\omega_1 - \omega_2)t - (k_1 - k_2)x]/2}\bigr].\notag \end{align} So we have a modulated wave again, a wave which travels with the mean frequency and the mean wave number, but whose strength is varying with a form which depends on the difference frequency and the difference wave number.

Now let us take the case that the difference between the two waves is relatively small. Let us suppose that we are adding two waves whose frequencies are nearly equal; then $(\omega_1 + \omega_2)/2$ is practically the same as either one of the $\omega$’s, and similarly for $(k_1 + k_2)/2$. Thus the speed of the wave, the fast oscillations, the nodes, is still essentially $\omega/k$. But look, the speed of propagation of the modulation is not the same! How much do we have to change $x$ to account for a certain amount of $t$? The speed of this modulation wave is the ratio \begin{equation} \label{Eq:I:48:16} v_M = \frac{\omega_1 - \omega_2}{k_1 - k_2}. \end{equation} The speed of modulation is sometimes called the group velocity. If we take the case that the difference in frequency is relatively small, and the difference in wave number is then also relatively small, then this expression approaches, in the limit, \begin{equation} \label{Eq:I:48:17} v_g = \ddt{\omega}{k}. \end{equation} In other words, for the slowest modulation, the slowest beats, there is a definite speed at which they travel which is not the same as the phase speed of the waves—what a mysterious thing!

2021.10.28: 인간의 한계
낱개가 아닌 덩어리로 움직인다는 거. 그룹 속도, 수학적으로는 2차원 표면/surface가 움직이는 거니까.
2022.4.12: 바이러스 존재여부 확인할 때, PCR로 복제 후 검사하듯이, 인간이 관찰할 수 있는 것은 덩어리 밖에 없다....
2022.7.13: 51장 waves를 읽는 중에 든 그룹 속도, speed of propagation of the modulation에 대하여
남녀가 투닥거리면서 동행하는 과정, 주식 정치 경제 사회의 많은 현상이 변화하는 걸 보면 오르락 내리락 하며 완만한 곡선을 만드는데, 그걸 modulation이라고 본다? disturbance가 있고 차차 stable하게 되는....

The group velocity is the derivative of $\omega$ with respect to $k$, and the phase velocity is $\omega/k$.

Let us see if we can understand why. Consider two waves, again of slightly different wavelength, as in Fig. 48–1. They are out of phase, in phase, out of phase, and so on. Now these waves represent, really, the waves in space travelling with slightly different frequencies also. Now because the phase velocity, the velocity of the nodes of these two waves, is not precisely the same, something new happens. Suppose we ride along with one of the waves and look at the other one; if they both went at the same speed, then the other wave would stay right where it was relative to us, as we ride along on this crest. We ride on that crest and right opposite us we see a crest; if the two velocities are equal the crests stay on top of each other. But it is not so that the two velocities are really equal. There is only a small difference in frequency and therefore only a small difference in velocity, but because of that difference in velocity, as we ride along the other wave moves slowly forward, say, or behind, relative to our wave. So as time goes on, what happens to the node? If we move one wave train just a shade forward, the node moves forward (or backward) a considerable distance. That is, the sum of these two waves has an envelope(* sort of 확장), and as the waves travel along, the envelope rides on them at a different speed. The group velocity is the speed at which modulated signals would be transmitted.

22.4.13: $\cos(\omega_1 t - k_1x)=\cos(\omega_1(t-\frac{k_1}{\omega_1}x)), \cos(\omega_2 t -k_2x)=\cos(\omega_2(t-\frac{k_2}{\omega_2}x))$ phase velocity를 얘기할 때, 헷갈린다.
페이스 속도가 $\frac{\omega}k$라면 $c$로 같아야 하는데... 다르다고 한다, 뭔 개소린지.
=> 한심한 인간아, $k=\frac{n\omega}c$와 $n$이 $\omega$와 관계 있다는 식 (48.12)이 있잖아. 제발 제대로 들여다 봐라, 넘겨짚지 말고. 1980년경 중섭이 새끼한테 그렇게 수모당하고도 정신 못차리니, 참. 제버릇 개 못 주나봐
Let $\frac{\omega_1}k_1=v_1, \frac{\omega_2}k_2=v_2.$ => $\cos(\omega_1(t-\frac{x}{v_1})), \cos(\omega_2(t-\frac{x}{v_2}))$
시간에 따른 crest 또는 node 위치를 계산하면, $\omega(t-\frac{x}v)=\frac{k\pi}2 => x=vt-\frac{k\pi}{2\omega}$, where $k$= 정수. 위치의 차이, $x_1-x_2=(v_1-v_2)t-{k\pi}(\frac{1}{2\omega_1}-\frac{1}{2\omega_2})$. 따라서,
① 속도가 같은 경우, $v_1=v_2 => x_1-x_2= -{k\pi}(\frac{1}{2\omega_1}-\frac{1}{2\omega_2})$, which means if the two velocities are equal the crests stay on top of each other.
② 다른 경우, $(v_1-v_2)t\ne 0$이므로 위치의 차이가 점점 벌어진다
7.29: 여기서 되처먹지 않게 space와 time을 동시에 고려하면서 헷갈렸는데... 핵심은 simply analyze what arrives at(or leaves from)
한쪽 파를 타고(ride along) 저쪽 파를 보는 경우, 같은 위치에 있는 파의 amplitude를 본다는 것.

If we made a signal, i.e., some kind of change in the wave that one could recognize when he listened to it, a kind of modulation, then that modulation would travel at the group velocity, provided that the modulations were relatively slow. (When they are fast, it is much more difficult to analyze.)

Now we may show (at long last), that the speed of propagation of x-rays in a block of carbon is not greater than the speed of light, although the phase velocity is greater than the speed of light. In order to do that, we must find $d\omega/dk$, which we get by differentiating (48.14): $dk/d\omega = 1/c + a/\omega^2c$. The group velocity, therefore, is the reciprocal of this, namely, \begin{equation} \label{Eq:I:48:18} v_g = \frac{c}{1 + a/\omega^2}, \end{equation} which is smaller than $c$! So although the phases can travel faster than the speed of light, the modulation signals travel slower, and that is the resolution of the apparent paradox! Of course, if we have the simple case that $\omega= kc$, then $d\omega/dk$ is also $c$. So when all the phases have the same velocity, naturally the group has the same velocity.

Let us now consider one more example of the phase velocity which is extremely interesting. It has to do with quantum mechanics. We know that the amplitude to find a particle at a place can, in some circumstances, vary in space and time, let us say in one dimension, in this manner: \begin{equation} \label{Eq:I:48:19} \psi = Ae^{i(\omega t -kx)}, \end{equation} where $\omega$ is the frequency, which is related to the classical idea of the energy through $E = \hbar\omega$, and $k$ is the wave number, which is related to the momentum through $p = \hbar k$. We would say the particle had a definite momentum $p$ if the wave number were exactly $k$, that is, a perfect wave which goes on with the same amplitude everywhere. Equation (48.19) gives the amplitude, and if we take the absolute square, we get the relative probability for finding the particle as a function of position and time. This is a constant, which means that the probability is the same to find a particle anywhere. Now suppose, instead, that we have a situation where we know that the particle is more likely to be at one place than at another. We would represent such a situation by a wave which has a maximum and dies out on either side (Fig. 48–6). (It is not quite the same as a wave like (48.1) which has a series of maxima, but it is possible, by adding several waves of nearly the same $\omega$ and $k$ together, to get rid of all but one maximum.)

Now in those circumstances, since the square of (48.19) represents the chance of finding a particle somewhere, we know that at a given instant the particle is most likely to be near the center of the “lump,” where the amplitude of the wave is maximum.

22.4.19: 'a situation, in those circumstances, lump', 48–4 localized wave trains, fig 48-6 등을 하나로 꿰뚫는 건, 입자는 기파의 덩어리
따라서 (48.19)를 기의 amplitude로, 입자는 그런 기들의 형체로, 즉 envelope, 흠... surface로 본다면, 위의 group velocity 또한 그 뜻에 어울린다.

If now we wait a few moments, the waves will move, and after some time the “lump” will be somewhere else. If we knew that the particle originally was situated somewhere, classically, we would expect that it would later be elsewhere as a matter of fact, because it has a speed, after all, and a momentum. The quantum theory, then, will go into the correct classical theory for the relationship of momentum, energy, and velocity only if the group velocity, the velocity of the modulation, is equal to the velocity that we would obtain classically for a particle of the same momentum.

It is now necessary to demonstrate that this is, or is not, the case. According to the classical theory, the energy is related to the velocity through an equation like \begin{equation} \label{Eq:I:48:20} E = \frac{mc^2}{\sqrt{1 - v^2/c^2}}. \end{equation} Similarly, the momentum is \begin{equation} \label{Eq:I:48:21} p = \frac{mv}{\sqrt{1 - v^2/c^2}}. \end{equation} That is the classical theory, and as a consequence of the classical theory, by eliminating $v$, we can show that \begin{equation*} E^2 - p^2c^2 = m^2c^4. \end{equation*} That is the four-dimensional grand result that we have talked and talked about, that $p_\mu p_\mu = m^2$; that is the relation between energy and momentum in the classical theory. Now that means, since these $E$’s and $p$’s are going to become $\omega$’s and $k$’s, by substitution of $E = \hbar\omega$ and $p = \hbar k$, that for quantum mechanics it is necessary that \begin{equation} \label{Eq:I:48:22} \frac{\hbar^2\omega^2}{c^2} - \hbar^2k^2 = m^2c^2. \end{equation} This, then, is the relationship between the frequency and the wave number of a quantum-mechanical amplitude wave representing a particle of mass $m$. From this equation we can deduce that $\omega$ is \begin{equation*} \omega = c\sqrt{k^2 + m^2c^2/\hbar^2}. \end{equation*} The phase velocity, $\omega/k$, is here again faster than the speed of light!

Now let us look at the group velocity. The group velocity should be $d\omega/dk$, the speed at which the modulations move. We have to differentiate a square root, which is not very difficult. The derivative is \begin{equation*} \ddt{\omega}{k} = \frac{kc}{\sqrt{k^2 + m^2c^2/\hbar^2}}. \end{equation*} Now the square root is, after all, $\omega/c$, so we could write this as $d\omega/dk = c^2k/\omega$. Further, $k/\omega$ is $p/E$, so \begin{equation*} v_g = \frac{c^2p}{E}. \end{equation*} But from (48.20) and (48.21), $c^2p/E = v$, the velocity of the particle, according to classical mechanics. So we see that whereas the fundamental quantum-mechanical relationship $E = \hbar\omega$ and $p = \hbar k$, for the identification of $\omega$ and $k$ with the classical $E$ and $p$, only produces the equation $\omega^2 - k^2c^2 = m^2c^4/\hbar^2$, now we also understand the relationships (48.20) and (48.21) which connected $E$ and $p$ to the velocity. Of course the group velocity must be the velocity of the particle if the interpretation is going to make any sense. If we think the particle is over here at one time, and then ten minutes later we think it is over there, as the quantum mechanics said, the distance traversed by the “lump,” divided by the time interval, must be, classically, the velocity of the particle.

We shall now bring our discussion of waves to a close with a few general remarks about the wave equation. These remarks are intended to give some view of the future—not that we can understand everything exactly just now, but rather to see what things are going to look like when we study waves a little more. First of all, the wave equation for sound in one dimension was \begin{equation*} \frac{\partial^2\chi}{\partial x^2} = \frac{1}{c^2}\,\frac{\partial^2\chi}{\partial t^2}, \end{equation*} where $c$ is the speed of whatever the wave is—in the case of sound, it is the sound speed; in the case of light, it is the speed of light. We showed that for a sound wave the displacements would propagate themselves at a certain speed. But the excess pressure also propagates at a certain speed, and so does the excess density. So we should expect that the pressure would satisfy the same equation, as indeed it does. We shall leave it to the reader to prove that it does. Hint: $\rho_e$ is proportional to the rate of change of $\chi$ with respect to $x$. Therefore if we differentiate the wave equation with respect to $x$, we will immediately discover that $\ddpl{\chi}{x}$ satisfies the same equation. That is to say, $\rho_e$ satisfies the same equation. But $P_e$ is proportional to $\rho_e$, and therefore $P_e$ does too. So the pressure, the displacements, everything, satisfy the same wave equation.

2022.4.17: 여기 핵심은 비례
$\frac{\partial^2\chi}{\partial x^2}=\frac{1}{c^2}\,\frac{\partial^2\chi}{\partial t^2}$의 양변을 $x$로 미분하면, => $\frac{\partial^3\chi}{\partial x^3} = \frac{1}{c^2}\,\frac{\partial^3\chi}{\partial x \partial t^2} => \text{미분을 뒤바꾸면} => \frac{\partial^2 {\frac{\partial \chi}{\partial x}}}{\partial x}= \frac{1}{c^2}\,\frac{\partial^3\chi}{\partial t^2 \partial x} =\frac{1}{c^2}\,\frac{\partial^2 {\frac{\partial \chi}{\partial x}}}{\partial t^2}$
식 (47.9) $\rho_e = -\rho_0\,\ddp{\chi}{x}$을 대입하면, excess density $\rho_e$는 위식을 만족하고, 식 (47.4) $P_e = \kappa\rho_e$이니 excess 압력도 위식을 만족.

Usually one sees the wave equation for sound written in terms of pressure instead of in terms of displacement, because the pressure is a scalar and has no direction. But the displacement is a vector and has direction, and it is thus easier to analyze the pressure.

The next matter we discuss has to do with the wave equation in three dimensions. We know that the sound wave solution in one dimension is $e^{i(\omega t - kx)}$, with $\omega = kc_s$, but we also know that in three dimensions a wave would be represented by $e^{i(\omega t - k_xx - k_yy - k_zz)}$, where, in this case, $\omega^2 = k^2c_s^2$, which is, of course, $(k_x^2 + k_y^2 + k_z^2)c_s^2$. Now what we want to do is to guess what the correct wave equation in three dimensions is. Naturally, for the case of sound this can be deduced by going through the same dynamic argument in three dimensions that we made in one dimension. But we shall not do that; instead we just write down what comes out: the equation for the pressure (or displacement, or anything) is \begin{equation} \label{Eq:I:48:23} \frac{\partial^2P_e}{\partial x^2} + \frac{\partial^2P_e}{\partial y^2} + \frac{\partial^2P_e}{\partial z^2} = \frac{1}{c_s^2}\, \frac{\partial^2P_e}{\partial t^2}. \end{equation} That this is true can be verified by substituting in $e^{i(\omega t - \FLPk\cdot\FLPr)}$. Clearly, every time we differentiate with respect to $x$, we multiply by $-ik_x$. If we differentiate twice, it is equivalent to multiplying by $-k_x^2$, so the first term would become $-k_x^2P_e$, for that wave. Similarly, the second term becomes $-k_y^2P_e$, and the third term becomes $-k_z^2P_e$. On the right, we get $-(\omega^2/c_s^2)P_e$. Then, if we take away the $P_e$’s and change the sign, we see that the relationship between $k$ and $\omega$ is the one that we want.

Working backwards again(* 음파 미분방정식 (48.23) => $(k_x^2 + k_y^2 + k_z^2)c_s^2$, 양자역학의 경우 거꾸로 (48.22) => 미분방정식), we cannot resist writing down the grand equation which corresponds to the dispersion equation (48.22) for quantum-mechanical waves. If $\phi$ represents the amplitude for finding a particle at position $x,y,z$, at the time $t$, then the great equation of quantum mechanics for free particles is this: \begin{equation} \label{Eq:I:48:24} \frac{\partial^2\phi}{\partial x^2} + \frac{\partial^2\phi}{\partial y^2} + \frac{\partial^2\phi}{\partial z^2} - \frac{1}{c^2}\, \frac{\partial^2\phi}{\partial t^2} = \frac{m^2c^2}{\hbar^2}\,\phi. \end{equation} First of all, the relativity character of this expression is suggested by the appearance of $x$, $y$, $z$ and $t$ in the nice combination relativity usually involves. Second, it is a wave equation which, if we try a plane wave, would produce as a consequence that $-k^2 + \omega^2/c^2 = m^2c^2/\hbar^2$, which is the right relationship for quantum mechanics. There is still another great thing contained in the wave equation: the fact that any superposition of waves is also a solution. So this equation contains all of the quantum mechanics and the relativity that we have been discussing so far, at least so long as it deals with a single particle in empty space with no external potentials or forces on it!

Now we turn to another example of the phenomenon of beats which is rather curious and a little different.
Imagine two equal pendulums which have, between them, a rather weak spring connection. They are made as nearly as possible the same length.

22.4.20: 연동 진자의 mathematical projection(물리적 현상을 수학적으로 표현하는 것)은 adding two waves
Chapter 49, 같은 mathematical proj 갖는 양자역학적 예

If we pull one aside and let go, it moves back and forth, and it pulls on the connecting spring as it moves back and forth, and so it really is a machine for generating a force which has the natural frequency of the other pendulum. Therefore, as a consequence of the theory of resonance, which we studied before, when we put a force on something at just the right frequency, it will drive it.

2024.4.21: Of course, it is a physical situation representing the 23.6 equation.
4.22: 움직임이 어떻게 작동하는가 이해할 좋은 예인 건 확실한데 이해가 안되는 건.... 좌우로의 움직임은 아래로만 향하는 움직임들과 함께 벽 역할하는 전자들에 의해 진자안을 좌충우돌하며 운동시키다 용수철을 통해 옆 진자로 진출하는 것으로 보인다. 근데 어떻게 진자가 멈출 정도로 하나도 남김없이 떠나는가? 일부는 헤매고 있어야 하지 않나 싶은 거다
4.25: 파동효과의 전자들이 빛 입자로 연결된 것처럼, 대대수 움직임들이 사슬처럼 연결되어 있어 좌충우돌하다 빠져나갈 구멍 발견하고 뱀처럼 이동하는 거... 6.29: 맞는 추론 ... see waveguide
7.24: see transistor+radio tube
11.28: 집안의 무선 인터넷 연결되는 걸 보면, 전자기파가 꼬리를 물고 뱀처럼 움직인다는 걸 확인시켜 준다

So, sure enough, one pendulum moving back and forth drives the other. However, in this circumstance there is a new thing happening, because the total energy of the system is finite, so when one pendulum pours its energy into the other to drive it, it finds itself gradually losing energy, until, if the timing is just right along with the speed, it loses all its energy and is reduced to a stationary condition! Then, of course, it is the other pendulum ball that has all the energy and the first one which has none, and as time goes on we see that it works also in the opposite direction, and that the energy is passed back into the first ball; this is a very interesting and amusing phenomenon. We said, however, that this is related to the theory of beats, and we must now explain how we can analyze this motion from the point of view of the theory of beats.

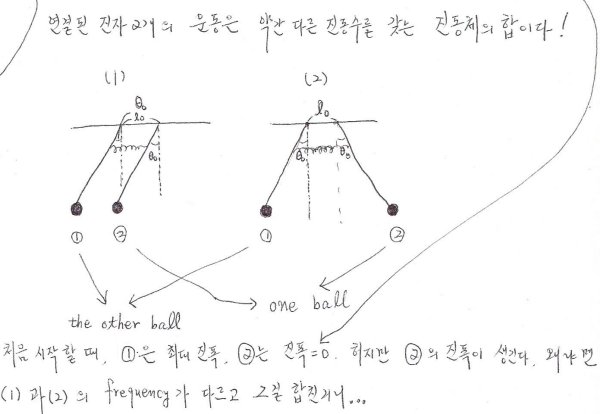
We note that the motion of either of the two balls is an oscillation which has an amplitude which changes cyclically.

2024.4.21: 2 진폭들 변화 관계식은 roughly 원을 그리는 거고, 움직임의 진폭이 커졌다 작아졌다 하며 왔다갔다하니 2 진자속에 갇힌 움직임 흐름.
진자 동영상: 보통실, 스프링 => 스프링 연결과 무관

Therefore the motion of one of the balls is presumably analyzable in a different way, in that it is the sum of two oscillations, present at the same time but having two slightly different frequencies. Therefore it ought to be possible to find two other motions in this system, and to claim that what we saw was a superposition of the two solutions, because this is of course a linear system. Indeed, it is easy to find two ways that we could start the motion, each one of which is a perfect, single-frequency motion—absolutely periodic. The motion that we started with before was not strictly periodic, since it did not last; soon one ball was passing energy to the other and so changing its amplitude; but there are ways of starting the motion so that nothing changes and, of course, as soon as we see it we understand why. For example, if we made both pendulums go together, then, since they are of the same length and the spring is not then doing anything, they will of course continue to swing like that for all time, assuming no friction and that everything is perfect. On the other hand, there is another possible motion which also has a definite frequency: that is, if we move the pendulums oppositely, pulling them aside exactly equal distances, then again they would be in absolutely periodic motion. We can appreciate that the spring just adds a little to the restoring force that the gravity supplies, that is all, and the system just keeps oscillating at a slightly higher frequency than in the first case. Why higher? Because the spring is pulling, in addition to the gravitation, and it makes the system a little “stiffer,” so that the frequency of this motion is just a shade higher than that of the other.

22.4.23: 2개중 하나를 잡아당겨 생기는 운동과 달리, 완벽한 주기의 운동을 만들 방법이 2가지 있다. 같은 방향으로 용수철이 늘어나지 않도록 동시에 움직이는 것과 반대로 움직이는 것. 당연히 진폭 불변
1. 진자운동을 2nd linear system으로 근사
2. 이 경우 초기조건(위치, 속도, 2nd이기에 이거로 족함)가 결정되면 그 궤도(motion)가 결정됨, 유크리드 제5공리의 일반화.
3. 헌데 위에서 언급하고 아래에 설명하였듯이, 2개 궤도를 조합하여 초기조건 맞는 궤도, 즉 모션을 만들면 바로 그것이 우리가 찾는 해라는 거(* Wronskian 보충 설명 및 수식 해법).

Thus this system has two ways in which it can oscillate with unchanging amplitude: it can either oscillate in a manner in which both pendulums go the same way and oscillate all the time at one frequency, or they could go in opposite directions at a slightly higher frequency.

Now the actual motion of the thing, because the system is linear, can be represented as a superposition of the two. (The subject of this chapter, remember, is the effects of adding two motions with different frequencies.) So think what would happen if we combined these two solutions. If at $t = 0$ the two motions are started with equal amplitude and in the same phase, the sum of the two motions means that one ball(②), having been impressed one way by the first motion and the other way by the second motion, is at zero, while the other ball(①), having been displaced the same way in both motions, has a large amplitude. As time goes on, however, the two basic motions proceed independently, so the phase of one relative to the other is slowly shifting. That means, then, that after a sufficiently long time, when the time is enough that one motion could have gone “$900\tfrac{1}{2}$” oscillations, while the other went only “$900$,” the relative phase would be just reversed with respect to what it was before. That is, the large-amplitude motion will have fallen to zero, and in the meantime, of course, the initially motionless ball will have attained full strength!

So we see that we could analyze this complicated motion either by the idea that there is a resonance and that one passes energy to the other, or else by the superposition of two constant-amplitude motions at two different frequencies.

2024.4.21: 파인만의 통찰, 물리 현상과 수학 등에 대한

1. 구체적 그림이 성공의 길
(1) line width 등 수학의 문제점, 증명이 아니라 연관성 아는 것이 중요,
(2) good enough approximation... fudging
 MRI, 피아노 조율, 렌즈 만들기, 색은 에너지 투사
 더 나아가 envelope 개념 확장, 벡터 공간을 추상적으로 확장한 것과는 좀 다르지만.

2. 인간 논리와 자연이 항상 부합하는 건 아니다
3. in a reasonable but erroneous way, somewhat subtle..., 열 전도
4. 과학의 참맛은 법칙이 당연하다는 것을 발견하는 거, 파동방정식 => 작용 반작용
5. Interference(간섭)과 Diffraction(회절)의 차이: question of usage
6. 편견을 버려라
7. 아는 것에서 출발... 개선, 뉴튼의 근사 접근
8. be consistent with everything else we know ...
9. 벡터 함수의 2차 도함수
10. What is the underlying unity of nature
11. detail보다는 idea가 중요
12. 정확한 물리적 상황 파악: 로렌쯔 축소

라며 수학적 논리, 형식 등 인위적인 것에 얽매이지 말 것을 누누히 강조했듯이, 수학과 물리를 오가는 해석의 commute가 중요, 그 예들

simply connected	conserve
equivariantly	resonantly
singularity	전자